Rules¶
Whatever method of use is selected, general rules are to be complied with in setting up the data.
The initial mesh¶
Mesh includes nodes, point-meshes, segments, triangles, quadrangles, tetrahedrons, hexahedrons and/or prisms. It may be of degree 1 or 2. It may be made up of several pieces. Meshes mixing volume meshed areas and surface meshed areas can definitely be processed. These areas may be adjacent or not. During the refining process there is no mesh adjustment. Therefore, the initial mesh should be as smooth as possible. Poor initial mesh would result in poor split meshes. Conversely, the initial mesh may be coarse. It merely needs to comply with the minimum initial conditions. Lastly, it would be desirable to have - from the very onset - proper representation of any curving borders. As border element splitting is carried out based on border approximation by the initial mesh, fine tracking of marked curves may not occur systematically. To remedy this, a specific module for 2D-border tracking is available.
Boundary conditions on limits and sources¶
Defining where boundary conditions or source operands are enforced has to be carried out on entities of dimensions similar to that of the phenomenon being represented. In other words, a one-off loading should be defined on a node. For 2D calculation, the definition of behaviors on the boundary is obtained through boundary edge characterizations rather than through boundary nodes. Also, in 3D, the behaviors on the outer walls of the area to be modeled are based on the triangles or the quadrangles making up the boundary. In so doing, one is sure to properly propagate the definitions as mesh is refined.
One should absolutely not use definitions of boundary conditions by nodes for this would make it impossible to properly represent the borders after adaptation. This is demonstrated in the example below.

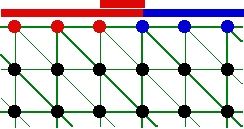
A case of fluid mechanics is to be modeled here, where a flow enters then exits a cavity. This is a 2D model, and boundary conditions are defined classically, through node characterization. On the zoom drawn below, red nodes are for walls and blue nodes for inlet, while black nodes are for free nodes.

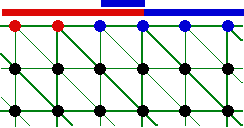
If the element needs to be split around the inlet area, new nodes are generated. The problem here is to find out to which category a new node located between a wall node or an inlet node belongs to. If – left-hand side case – the wall gets priority, everything is fine. Conversely, if – right-hand side case – it is the inlet that gets priority, there is a problem: this results in artificially expanding the inlet, therefore distorting the calculation!
The management of priorities between data soon becomes impossible : exclusive conventions for all HOMARD-related calculation softwares would have to be set up, while dealing with a combination of many possibilities. Moreover, in 3D, this technique for managing priorities leads to a deadlock. Try and imagine updating characterizations for nodes resulting from the splitting of tetrahedrons in the angle of the domain. Very quickly, it becomes impossible to choose between blue, red and green.

The only viable solution consists in defining boundary conditions on boundary elements. Going back to our 2D example for fluid mechanics, the wall or inclet characteristics are assigned to the boundary edges. In the calculation software, the program can very easily transfer information on edges towards border summits.
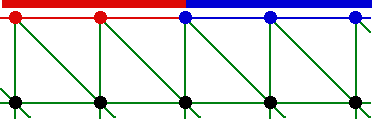
If the mesh refinement is carried out as previously, the new edges take on the same characterization as those out of which they arise : one split wall edge results in two wall edges, and one split inlet edge results in two inlet edges. Consequently, the calculation software has no difficulty setting up the right data on border nodes.

The strategy for the adaptation¶
There is a choice between several types of refinement and unrefinement :
by filtering error indications through a given threshold : all of the elements involving an error superior to the high threshold are split and all of those involving an error lower than the low threshold are unrefined. Then, splitting occurs again until mesh does not contain hanging nodes.
by filtering error indications through thresholds that depends on the error : all of the elements involving an error superior to the mean of the error with a shift are split. Then, splitting occurs again until mesh does not contain hanging nodes.
by filtering with percentage of elements. The x% of the elements with the highest error are split and the y% with the lowest errors are unrefined.
by only using the refinement process, filtering with an high threshold.
vice versa by only using the unrefinement process, filtering with a low threshold.
uniform; no error indicator is taken into account, and mesh is entirely split : every triangle is split into 4 sections, every quadrangle is split into 4 sections, every tetrahedron is split into 8 sections, every prism is split into 8 sections, and every hexahedron is split into 8 sections. Beware! The resulting mesh volume may be huge.
The error indicator¶
Most of the time, the error indicator is a real-value field defined by element. It is one of the results of the calculation software. The selection of the elements to be split is carried out by comparing the value of the indicator to a given threshold. HOMARD accommodates two extensions to this standard: an error indicator expressed on node and/or error indicator under integer form. Whenever the indicator is provided over a node, HOMARD assigns the highest error value encountered on the element nodes to each element. Whenever the indicator is under integer form, the convention is that 1 is for refinement requests and 0 for no action. There is no requirement to provide a value for each and every element: if no value is assigned to an element, HOMARD treats this element according to the preferences of the case.
The interpolation of the fields¶
HOMARD is able to update fields which are expressed over the mesh. Two cases are available :
If the field is expressed by nodes, HOMARD will produce a new field by node, following this method. When a node is active in both meshes, before and after adaptation, the field value is kept. If the node is new, the value of the field is obtained from its values over neighbours, interpolating the field according to the mesh degree and to the choice P1, P2 or iso-P2.
If the field is expressed as a constant by element, HOMARD will produce a new field by element. The method depends on the characteristics of the field: intensive, as a density, or extensive, as a mass. When the element is active in both elements, before and after adaptation, the field value is kept. If the element is produced by element cutting, the field value is the one of the parent element in the case ‘intensive’; it is the value with the ratio of the volumes of parent and child elements in the case ‘extensive’. If the element is produced by mesh coarsening, the field value is the mean value over the previous child elements in the case ‘intensive’; it is the sum of the values over the previous child elements with the ratio of the volumes of parent and child elements in the case ‘extensive’.
These updating techniques are based on scalar fields. If a vector field is transmitted to HOMARD through the MED files, each component is considered as a independent scalar field. Then, the new vector field is built, gathering all the new scalar components.