YACS¶
Using a YACS scheme allows the coupling between a computation and an adaptation as described into Introduction. This coupling can be repeated inside a loop as long as a criteria for the convergence is reached for instance. Many ways are available to program a YACS scheme. The solution that is shown here is correct but many others are too!
In this part, an extensive description of a schema YACS is available.
Note
The module HOMARD proposes an automatic creation of a schema YASC starting from a defined case. To do that, see The schema YACS
Introduction¶
Here is the description of a scheme for a computation in which a value is to be stabilized. The computation starts over an initial mesh, then HOMARD makes an adaptation. A new computation is done over this new mesh and its result is analyzed. Depending on this analysis, the coupling goes on or does not. The general look of the scheme is this one:
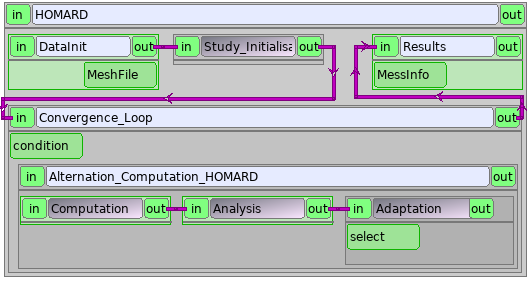
Note
Among all the treated data, certain are unchanging: the name of the directory of calculation, the name of the case, the name of the hypothesis of adaptation, etc. It was chosen to impose them ‘hard’ in the various parameters of service or within the scripts python. We could also define them a priori in a node PresetNode and then pass on them by links. We did not hold this solution because it increases strongly the number of parameters and links attached to every node. It is very penalizing for the legibility of the scheme. The only data which are going to circulate are the ones been imperative by the description of the service and those that evolve during the execution of the scheme.
The boxes¶
The main boxes are:
DataInit : initialisation of the initial mesh
Study_Initialisation : launching of the module HOMARD inside SALOME
Convergence_Loop : gestion of the loop computation/adaptation
Results : final information
DataInit¶

This box is type PresetNode’s elementary node. Its only function is to initialize the variable MeshFile that contains the name of the file of the initial mesh.
<datanode name="DataInit">
<parameter name="MeshFile" type="string">
<value><string>/home/D68518/HOMARD_SVN/trunk/training/tet_aster_ther/maill.00.med</string></value>
</parameter>
</datanode>
Study_Initialisation¶
The box Study_Initialisation launches the component HOMARD inside SALOME. It is a block consisted of two parts, that are invariable whatever is the envisaged application:
StudyCreation : python node
UpdateStudy : service of the component HOMARD

The python node StudyCreation initialize the SALOME study that is given through the output:
<inline name="StudyCreation">
<script><code><![CDATA[
import orbmodule
import SALOMEDS_idl
import HOMARD
import HOMARD_Gen_idl
import HOMARD_Cas_idl
import HOMARD_Iteration_idl
import HOMARD_Hypothesis_idl
import HOMARD_Zone_idl
import HOMARD_Boundary_idl
clt = orbmodule.client()
CurrentStudy = clt.Resolve("/Study")
]]></code></script>
</inline>
The service UpdateStudy connects this study to an instance of HOMARD.
<service name="UpdateStudy">
<component>HOMARD</component>
<load container="DefaultContainer"/>
<method>UpdateStudy</method>
</service>
Convergence_Loop¶
The box Convergence_Loop is type WhileLoop. The condition is initialized with 1: the internal block Alternation_Computation_HOMARD is executed. Within this block, we calculate and we adapt the mesh; when the process has to stop either as a result of error, or by convergence, the condition passes to 0. The loop ends and we pass in the following box, Results.

Results¶
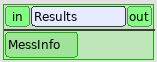
This box is a node python that takes in input a character string, MessInfo. If everything passed well, this message is empty. A window QT appears to confirm the convergence. If there was a problem, the message contains messages emitted during the calculations. The window QT shows this message.
<inline name="Results">
<script><code><![CDATA[
from PyQt5 import QtWidgets
import sys
app = QtWidgets.QApplication(sys.argv)
MessageBoxTitle = "Results"
if MessInfo == "" :
MessInfo = "The convergence is reached."
QtWidgets.QMessageBox.information(None, MessageBoxTitle, MessInfo)
else :
QtWidgets.QMessageBox.critical(None, MessageBoxTitle, MessInfo)
]]></code></script>
<inport name="MessInfo" type="string"/>
</inline>
Loop for the calculations¶

This box is a block that manages the computation, the adaptation and the analysis.
Computation¶

This box is a node python that is going to drive the calculation. In input, we find the number of the calculation (0 at first) and the name of the file which contains the mesh on which to calculate. In output, we find an integer which represents the error on this calculation (0 so everything goes well) and a dictionary python gathering the results of the calculation. The body of the node is established by the launch of a script python that activates the calculation.
<script><code><![CDATA[
import sys
import os
#
rep_calc = "/home/D68518/HOMARD_SVN/trunk/training/tet_aster_ther"
rep_script = os.path.dirname("/home/D68518/HOMARD_SVN/trunk/training/script")
sys.path.append(rep_script)
from ScriptAster import Script
#
argu = ["-v"]
argu.append("--rep_calc=" + rep_calc)
argu.append("--num=%d" % numCalc)
argu.append("--mesh_file=" + MeshFile)
#
Script_A = Script(argu)
#
Error, message_erreur, dict_resu = Script_A.compute ()
#
dict_resu["rep_calc"] = rep_calc
#
]]></code></script>
In this example, we must define:
rep_calc : the directory in which will be executed the calculation.
rep_script : the directory in which is the python that will launch the calculation. This directory is to be added to the PATH. From this directory, we shall import Script from the file ScriptAster.py
The python Script is programmed as the user wishes it so that the calculation can be made on the current mesh. According to the mode of launch of the code of calculation, we can need other information, as the number of the calculation or the directory of the calculation for example. The freedom is total. In our case, the arguments of input are the name of the file of mesh, the number of the calculation and the directory of calculation. They are given in a list python: [“–rep_calc=rep_calc”, “–num=numCalc”, “–mesh_file=MeshFile”] ].
On the other hand the output of the script has to obey the following rule. We get back a code of error, an error message and a dictionary. This dictionary contains necessarily the following keys:
“FileName” : the name of the file that contains the results of the calculation
“V_TEST” : the value the convergence of which we want to test
Adaptation¶

The box Adaptation is a Switch node driven by the code of error of the previous calculation. If this code is nil, YACS will activate the box Adaptation_HOMARD that will launch the adaptation. If the code is not nil, we pass directly in the box Loop_Stop.
Adaptation_HOMARD¶
The first task tries to execute concern the initialization of the data necessary for HOMARD in the box HOMARD_Initialisation. This box is a switch node driven by the number of the calculation. In the starting up, the number is nil and YACS activates the box Iter_1.
Iter_1¶

This box begins by creating the case HOMARD by calling the CreateCase service.
<service name="CreateCase">
<node>Study_Initialisation.UpdateStudy</node>
<method>CreateCase</method>
<inport name="CaseName" type="string"/>
<inport name="MeshName" type="string"/>
<inport name="FileName" type="string"/>
<outport name="return" type="HOMARD_Cas"/>
</service>
The name of the case CaseName is imposed on “Computation”. The name of the case MeshName is imposed on “BOX”. The parameters of input FileName arise from the output of the previous calculation. The parameter of output is an instance of case.
<parameter>
<tonode>Convergence_Loop.Alternation_Computation_HOMARD.Adaptation.p0_Adaptation_HOMARD.HOMARD_Initialisation.p1_Iter_1.CreateCase</tonode><toport>CaseName</toport>
<value><string>Computation</string></value>
</parameter>
<parameter>
<tonode>Convergence_Loop.Alternation_Computation_HOMARD.Adaptation.p0_Adaptation_HOMARD.HOMARD_Initialisation.p1_Iter_1.CreateCase</tonode><toport>MeshName</toport>
<value><string>BOX</string></value>
</parameter>
The options of this case must be now given. It is made by the node python CaseOptions. It is imperative to give the directory of calculation. We shall look at the description of the functions in The case. In output, we get back the instance of the iteration corresponding to the initial state of the case.
<inline name="Case_Options">
<script><code><![CDATA[
import os
# Directory for the adaptation
DirName = "/home/D68518/HOMARD_SVN/trunk/training/tet_aster_ther/HOMARD"
Case.SetDirName(DirName)
Case.SetConfType(1)
# Associated iteration #0
Iter0 = Case.GetIter0()
]]></code></script>
<inport name="Case" type="HOMARD_Cas"/>
<outport name="Iter0" type="HOMARD_Iteration"/>
</inline>
Finally, a hypothesis is created by calling the CreateHypothese service. The parameter of output is an instance of hypothese.
Homard_Exec¶
Once initialized, the adaptation can be calculated. It is the goal of the Homard_Exec box, in the form of a script python.

The directory of calculation is recovered. The name of the mesh is given.
<inline name="HOMARD_Exec">
<script><code><![CDATA[
import os
# Directory for the computation
DirName = "/scratch/D68518/HOMARD_SVN/trunk/training/tet_aster_ther"
MeshName = "BOX"
../..
]]></code></script>
<inport name="NumAdapt" type="int"/>
<inport name="LastIter" type="HOMARD_Iteration"/>
<inport name="Hypo" type="HOMARD_Hypothesis"/>
<inport name="dict_resu" type="pyobj"/>
<outport name="OK" type="bool"/>
<outport name="MessInfo" type="string"/>
<outport name="MeshFile" type="string"/>
</inline>
The hypothesis transmitted in input parameter characterized (look The hypothesis) :
# . Name of the hypothesis
# ------------------------
HypoName = Hypo.GetName()
#
# . Options
# ---------
# . Type of adaptation: refinement and unrefinement driven by a field
Hypo.SetAdapRefinUnRef(1, 1, 1)
# . Name of the field
Hypo.SetField("ERREUR")
# . Values over meshes
Hypo.SetUseField(0)
# . Compoment
Hypo.AddComp("ERTABS")
# . Driving options
Hypo.SetRefinThr(4, 3)
Hypo.SetUnRefThr(4, 4)
#
# . Interpolation
Hypo.SetTypeFieldInterp(2)
Hypo.AddFieldInterp("TEMPERATURE")
#
# . Minimum limit size of the meshes
aux = 0.0015
Hypo.SetDiamMin(aux)
It is necessary to establish a name for the future iteration. To make sure that the name was never used, one installs a mechanism of incremental naming starting from the name of the initial iteration. As this initial name is the name of the initial mesh, one obtains a succession of names in the form: M_001, M_002, M_003, etc
# Name of the next iteration
# ==========================
# . Name of the previous iteration
LastIterName = LastIter.GetName()
aux = '%03d' % NumAdapt
# . At iteration #1, addition
if NumAdapt == 1 :
IterName = LastIterName + "_" + aux
# . Then, substitution
else :
IterName = LastIterName[:-3] + aux
The iteration is supplemented : hypothesis, future mesh, field (look The iteration) :
# Creation of the iteration
# =========================
Iter = LastIter.NextIteration(IterName)
#
# Options of the iteration
# ========================
# . Association de l'hypothese
Iter.AssociateHypo(HypoName)
#
# . The name of the next mesh
Iter.SetMeshName(MeshName)
#
# . The file of the next mesh
aux = '%02d' % NumAdapt
MeshFile = os.path.join (DirName, "maill."+aux+".med")
Iter.SetMeshFile(MeshFile)
#
# . The file for the fields
FileName = dict_resu["FileName"]
Iter.SetFieldFile(FileName)
The iteration is calculated. If it were correct, variable OK equals 1: one will be able to continue the execution of the scheme. If there were a problem, variable OK equals 0 to mean that calculation must stop; an error message then is given.
# Computation
# ===========
Error = Iter.Compute(1,1)
#
# The loops stops if problem
# ==========================
if Error :
OK = 0
MessInfo = "Error in HOMARD in the adaptation # %d" % NumAdapt
else :
OK = 1
MessInfo = " "
After this execution, the process leaves the Adaptation_HOMARD node, then Adaptation node. One arrives then at the node of analysis.
Iter_n¶

For the following passing in the block of adaptation, it is necessary to recover:
the last created iteration: service LastIteration (look The iteration)
the created hypothesis: service GetHypothesis (look The hypothesis)
One passes then in the Homard_Exec node to calculate the new mesh.
Loop_Stop¶
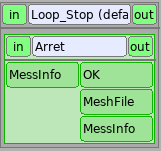
The Loop_Stop block is present to only make forward variables because the input parameters of the nodes must always be filled. It is a very simple python:
<bloc name="Loop_Stop">
<inline name="Arret">
<script><code><![CDATA[
OK = 0
MeshFile = " "
]]></code></script>
<inport name="MessInfo" type="string"/>
<outport name="OK" type="bool"/>
<outport name="MeshFile" type="string"/>
<outport name="MessInfo" type="string"/>
</inline>
</bloc>
Analysis¶

The Analysis block is a script python which ensures the complete control of the process by examining the causes of possible error successively.
<inline name="Analysis">
<script><code><![CDATA[
global NumCalc
global resu1
# Default values
NumCalcP1 = NumCalc + 1
FileName = " "
#
NbCalcMax = 5
#
MessInfo = None
Error = 0
while not Error :
../..
]]></code></script>
<inport name="NumCalc" type="int"/>
<inport name="ErrCalc" type="int"/>
<inport name="dict_resu" type="pyobj"/>
<outport name="Error" type="int"/>
<outport name="NumCalcP1" type="int"/>
<outport name="FileName" type="string"/>
<outport name="MessInfo" type="string"/>
</inline>
One starts by analyzing the return of the computer code:
# If the computation failed, stop:
#
if ErrCalc :
MessInfo = "Computation error # %d" % ErrCalc
Error = abs(ErrCalc)
break
Checking of the presence of the name of the result file in the dictionary of the results:
# If the file is not defined, stop:
#
if ( "FileName" in dict_resu ) :
FileName = dict_resu["FileName"]
else :
MessInfo = "The file for the mesh is not defined."
Error = -2
break
Checking of convergence. That supposes that the value to be tested is present in the dictionary under the key ‘V_TEST’. Here, one set up a test on the variation of the value of one calculation at the other. With the first passage, nothing is tested. In the following passing, one tests if the relative variation is lower than 1 thousandths. One could have set up an absolute test if one had recovered a total level of error for example.
# If the criterion is satisfied, stop:
#
if ( "V_TEST" in dict_resu ) :
valeur_v = dict_resu["V_TEST"]
if NumCalc == 0 :
resu1 = [valeur_v]
else :
resu1.append(valeur_v)
if NumCalc > 2 :
solu_m1 = resu1[-2]
rap = ( resu1[-1] - solu_m1 ) / solu_m1
if abs(rap) < 0.001 :
MessInfo = ""
Error = -9999
break
else :
MessInfo = "The value for the test is not available."
Error = -3
break
#
# If the maximum number of adaptations is reached, stop:
Lastly, it is checked that a maximum nomber of adaptations is not exceeded:
# If the maximum number of adaptations is reached, stop:
#
if NumCalc > NbCalcMax :
MessInfo = "The maximum number of adaptations is reached: %d" % NbCalcMax
Error = -1
break
Use this scheme¶
- To reproduce this example, download:
It should be adapted to simulation considered. In particular, it is necessary:
to adjust the names of the files and the directories
to provide a script of launching of calculation respecting the instructions evoked herebefore
to choose the hypothesis of driving of the adaptation
to set up the test of stop