3. [DocT] Methodology to elaborate a Data Assimilation or Optimization study¶

This section presents a generic methodology to build a Data Assimilation or Optimization study. It describes the conceptual steps to build autonomously this study. It is not dependent of any tool, but the ADAO module allows to set up efficiently such a study. Notations are the same than the ones used in [DocT] A brief introduction to Data Assimilation and Optimization.

3.1. Logical procedure for a study¶

For a generic Data Assimilation or Optimization study, the main methodological steps may be as follows, each of which is detailed in the following section:

STEP 1: Specify the resolution of the physical problem and the parameters to adjust
STEP 2: Specify the criteria for physical results qualification
STEP 3: Identify and describe the available observations
STEP 4: Specify the DA/Optimization modeling elements (covariances, background…)
STEP 5: Choose the optimization algorithm and its parameters
STEP 6: Conduct the optimization calculations and get the results
STEP 7: Exploit the results and qualify their physical properties

To illustrate these methodological steps from the perspective of a study applied to an industrial system or problem, the following diagram depicts these methodological steps in relation to the typical steps in a study:

The methodological steps required during a study approach applied to an industrial system or problem

3.2. Detailed procedure for a study¶

3.2.1. STEP 1: Specify the resolution of the physical problem and the parameters to adjust¶

An essential knowledge about the studied physical system is the numerical simulation. It is often available through calculation case(s), and symbolized as a simulation operator (previously included in $H$ ). A standard calculation case gathers model hypothesis, numerical implementation, computing capacities, etc. in order to represent the behavior of the physical system. Moreover, a calculation case is characterized for example by its computing time and memory requirements, its data and results sizes, etc. The knowledge of all these elements is of primary importance in the setup of the data assimilation or optimization study.

To state correctly the study, one have also to choose the optimization unknowns in the simulation. Frequently, this can be through physical models of which the parameters can be adjusted. Moreover, it is always useful to add some knowledge of sensitivity, for example of the numerical simulation to the parameters that can be adjusted. More general elements, like stability or regularity of the simulation with respect to the unknown inputs, are also of great interest.

Technically, optimization methods can require gradient information of the simulation with respect to unknowns. In this case, explicit gradient code has to be given, or numerical gradient has to be tuned. Its quality is in relation with the simulation code stability or regularity, and it has to be checked carefully before establishing optimization calculations. Specific conditions has to be used for these checkings.

An observation operator is always required, in complement of the simulation operator, or sometimes directly included in. This observation operator, denoted as $H$ , has to convert the numerical simulation outputs into something that is directly comparable to observations. It is an essential operator, as it is the real practical way to compare simulations and observations. It is usually done by sampling, projection or integration, of the simulation outputs, but it can be more complicated. Often, because the observation operator directly follows the simulation one in simple data assimilation schemes, this observation operator heavily use the post-processing and extraction capacities of the simulation code.

3.2.2. STEP 2: Specify the criteria for physical results qualification¶

Because the studied system are real physical ones, it is of great importance to express the physical information that can help to qualify a simulated system state. There are two main types of such information that leads to criteria allowing qualification and quantification of optimization results.

First, coming from mathematical or numerical knowledge, a lot of standard criteria allow to qualify, relatively or in absolute, the interest of an optimized state. For example, balance equations or equation closing conditions are good complementary measures of system state quality. Well chosen criteria like RMS, RMSE, field extrema, integrals, etc. are also of great interest to assess optimized state quality.

Second, coming from physical or experimental knowledge, valuable information can be obtained from the meaning of optimized results. In particular, physical validity or technical interest can assess of the numerical results of the optimization.

In order to get helpful information from these two main types of knowledge, it is recommended, if possible, to build numerical criteria to ease the assessment of global quality of numerical results.

3.2.3. STEP 3: Identify and describe the available observations¶

As the second main source of knowledge of the physical system to be studied, the observations, or measures, denoted as $\mathbf{y}^o$ , has to be properly described. The quality of the measures, their intrinsic errors, their special features, are worth to know, in order to introduce these information in the data assimilation or optimization calculations.

The observations have not only to be available, but also to be efficiently introduced in the numerical framework of calculation or optimization. So the computing environment giving access to the observations is of great importance to smooth the effective use of various measures and sources of measures, and to promote extensive tests using measures. Computing environment covers availability in database or not, data formats, application interfaces, etc.

3.2.4. STEP 4: Specify the DA/Optimization modeling elements (covariances, background…)¶

Additional Data Assimilation or Optimization modeling elements allows to improve information about the fine physical representation of the studied system.

The a-priori knowledge of the system state can be modelized using the background, denoted as $\mathbf{x}^b$ , and the background error covariance matrix, denoted as $\mathbf{B}$ . These information are extremely important to complete, in particular in order to obtain meaningful results from Data Assimilation.

On the other hand, information on observation errors can be used to fill the observation error covariance matrix denoted as 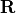$\mathbf{R}$ . As for $\mathbf{B}$ , it is recommended to use carefully checked data to fill these covariance matrices.

In case of dynamic simulation, one has to define also an evolution operator and the associated evolution error covariance matrix.

3.2.5. STEP 5: Choose the optimization algorithm and its parameters¶

Data Assimilation or Optimization requires to solve an optimization problem, more often modelized as a minimization problem. Depending on the availability of the gradient of the cost function with respect to the optimization parameters, recommended class of methods are different. Variational or locally linearized minimization methods requires this gradient. On the opposite, derivative free optimization methods doesn’t requires this gradient, but present usually a really higher computational price.

Inside a class of optimization methods, for each method, there is usually a trade-off between the “generic capacity of the method” and its “particular performance on a specific problem”. Most generic methods, as for example variational minimization using the Calculation algorithm “3DVAR”, present remarkable numerical properties of efficiency, robustness and reliability, that leads to recommend it independently of the problem to solve. Moreover, it is generally difficult to tune the parameters of an optimization method, so the most robust one is often the one with the less parameters. Finally, at least for the beginning, it is recommended to use the most generic methods and to change the less possible the known default parameters.

3.2.6. STEP 6: Conduct the optimization calculations and get the results¶

After setting up the Data Assimilation or Optimization study, the calculation has to be done in an efficient way.

Because optimizing usually involves a lot of elementary physical simulation of the system, the calculations are often done in High Performance Computing (HPC) environment to reduce the overall user time. Even if the optimization problem is small, the physical system simulation time can be long, requiring efficient computing resources. These requirements have to be taken into account early enough in the study procedure to be satisfied without needing too much effort.

For the same reason of hight computing requirements, it is important to carefully prepare the outputs of the optimization procedure. The optimal state is the main required information, but a lot of other special information can be obtained during or at the end of the optimization process: error evaluations, intermediary states, quality indicators, etc. All these information, sometimes requiring additional processing, have to be known and asked at the beginning of the optimization process.

3.2.7. STEP 7: Exploit the results and qualify their physical properties¶

Once getting the results, they have to be interpreted in terms of physical and numerical meaning. Even if the optimization calculation always give a new optimal state at least as good as the a priori one, and most hopefully better, this optimal state has for example to be checked with respect to the quality criteria identified when STEP 2: Specify the criteria for physical results qualification. This can lead to physical, statistical or numerical studies in order to assess the interest of the optimal state to represent the physical system.

Besides this analysis that has to be done for each Data Assimilation or Optimization study, it can be worth to exploit the optimization results as part of a more complete study of the physical system of interest.

3.3. To test a data assimilation chain: the twin experiments¶

When developing an assimilation study, the various steps described above form what is known as a “data assimilation chain”. The testing and analysis of this chain are critical to assess the confidence in the overall approach of the study.

For this purpose, twin experiments are a classical and very useful tool, which allows to place oneself in a particular environment where simulations and expected errors can be controlled. Thus, methodological or numerical difficulties can be separated and identified, then corrected.

The twin experiment approach can be schematized by the following figure, which presents the objective and the means of the approach:

The twin experiment approach to test and analyze a data assimilation (DA) chain

To simplify, the general approach to using the twin experiments methodology can be described as follows:

we choose in an arbitrary way a state called “true”, which must be valid for the simulation ;
we then elaborate “pseudo-observations” from the simulation of the true state, by sampling the simulation in a similar way to real observations ;
we eventually incorporate noise, either in the true state, or in the pseudo-observations, or in the computational chain, and this in a coherent way with the hypotheses of elaboration of the chain, to see its effect on a specific part of the chain ;
we then analyze, according to the noise assumptions applied, the ability of the chain to recover the true state or expected differences.

Thus, the methodology of twin experiments, applied several times and with different controlled hypotheses of noise or error, allows to verify step by step each component of the complete data assimilation chain.