13.1. Calculation algorithm “3DVAR”¶

13.1.1. Description¶

This algorithm performs a state estimation by variational minimization of the classical $J$ function in static data assimilation:

$J(\mathbf{x})=(\mathbf{x}-\mathbf{x}^b)^T.\mathbf{B}^{-1}.(\mathbf{x}-\mathbf{x}^b)+(\mathbf{y}^o-H(\mathbf{x}))^T.\mathbf{R}^{-1}.(\mathbf{y}^o-H(\mathbf{x}))$

which is usually designed as the “3D-Var” function (see for example [Talagrand97]). The terms “3D-Var”, “3D-VAR” and “3DVAR” are equivalent.

There exists various variants of this algorithm. The following stable and robust formulations are proposed here:

“3DVAR” (3D Variational analysis, see [Lorenc86], [LeDimet86], [Talagrand97]), original classical algorithm, extremely robust, which operates in the model space,
“3DVAR-VAN” (3D Variational Analysis with No inversion of B, see [Lorenc88]), similar algorithm, which operates in the model space, avoiding inversion of the covariance matrix B (except in the case where there are bounds.),
“3DVAR-Incr” (Incremental 3DVAR, see [Courtier94]), cheaper algorithm than the previous ones, involving an approximation of non-linear operators,
“3DVAR-PSAS” (Physical-space Statistical Analysis Scheme for 3DVAR, see [Courtier97], [Cohn98]), algorithm sometimes cheaper because it operates in the observation space, involving an approximation of non-linear operators, not allowing to take into account bounds.

It is highly recommended to use the original “3DVAR”. The “3DVAR” and “3DVAR-Incr” algorithms (and not the others) explicitly allow the modification of the initial point of their minimization, even if it is not recommended.

This mono-objective optimization algorithm is naturally written for a single estimate, without any dynamic or iterative notion (there is no need in this case for an incremental evolution operator, nor for an evolution error covariance). In ADAO, it can also be used on a succession of observations, placing the estimate in a recursive framework similar to a Calculation algorithm “KalmanFilter”. A standard estimate is made at each observation step on the state predicted by the incremental evolution model, knowing that the state error covariance remains the background covariance initially provided by the user. To be explicit, unlike Kalman-type filters, the state error covariance is not updated.

An extension of 3DVAR, coupling a “3DVAR” method with a Kalman ensemble filter, allows to improve the estimation of a posteriori error covariances. This extension is obtained by using the “E3DVAR” variant of the filtering algorithm Calculation algorithm “EnsembleKalmanFilter”.

13.1.2. Optional and required commands¶

The general required commands, available in the editing user graphical or textual interface, are the following:

Background: Vector. The variable indicates the background or initial vector used, previously noted as $\mathbf{x}^b$ . Its value is defined as a “Vector” or “VectorSerie” type object. Its availability in output is conditioned by the boolean “Stored” associated with input.

BackgroundError: Matrix. This indicates the background error covariance matrix, previously noted as $\mathbf{B}$ . Its value is defined as a “Matrix” type object, a “ScalarSparseMatrix” type object, or a “DiagonalSparseMatrix” type object, as described in detail in the section Requirements to describe covariance matrices. Its availability in output is conditioned by the boolean “Stored” associated with input.

Observation: List of vectors. The variable indicates the observation vector used for data assimilation or optimization, and usually noted $\mathbf{y}^o$ . Its value is defined as an object of type “Vector” if it is a single observation (temporal or not) or “VectorSeries” if it is a succession of observations. Its availability in output is conditioned by the boolean “Stored” associated in input.

ObservationError: Matrix. The variable indicates the observation error covariance matrix, usually noted as 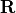$\mathbf{R}$ . It is defined as a “Matrix” type object, a “ScalarSparseMatrix” type object, or a “DiagonalSparseMatrix” type object, as described in detail in the section Requirements to describe covariance matrices. Its availability in output is conditioned by the boolean “Stored” associated with input.

ObservationOperator: Operator. The variable indicates the observation operator, usually noted as $H$ , which transforms the input parameters $\mathbf{x}$ to results $\mathbf{y}$ to be compared to observations $\mathbf{y}^o$ . Its value is defined as a “Function” type object or a “Matrix” type one. In the case of “Function” type, different functional forms can be used, as described in the section Requirements for functions describing an operator. If there is some control $U$ included in the observation, the operator has to be applied to a pair $(X,U)$ .

The general optional commands, available in the editing user graphical or textual interface, are indicated in List of commands and keywords for data assimilation or optimization case. Moreover, the parameters of the command “AlgorithmParameters” allows to choose the specific options, described hereafter, of the algorithm. See Description of options of an algorithm by “AlgorithmParameters” for the good use of this command.

The options are the following:

Bounds

List of pairs of real values. This key allows to define pairs of upper and lower bounds for every state variable being optimized. Bounds have to be given by a list of list of pairs of lower/upper bounds for each variable, with a value of None each time there is no bound. The bounds can always be specified, but they are taken into account only by the constrained optimizers.

Example: {"Bounds":[[2.,5.],[1.e-2,10.],[-30.,None],[None,None]]}

CostDecrementTolerance

Real value. This key indicates a limit value, leading to stop successfully the iterative optimization process when the cost function decreases less than this tolerance at the last step. The default is 1.e-7, and it is recommended to adapt it to the needs on real problems. One can refer to the section describing ways for Convergence control for calculation cases and iterative algorithms for more detailed recommendations.

Example: {"CostDecrementTolerance":1.e-7}

EstimationOf

Predefined name. This key allows to choose the type of estimation to be performed. It can be either state-estimation, with a value of “State”, or parameter-estimation, with a value of “Parameters”. The default choice is “Parameters”.

Example: {"EstimationOf":"Parameters"}

GradientNormTolerance

Real value. This key indicates a limit value, leading to stop successfully the iterative optimization process when the norm of the gradient is under this limit. It is only used for non-constrained optimizers. The default is 1.e-5 and it is not recommended to change it.

Example: {"GradientNormTolerance":1.e-5}

InitializationPoint

Vector. The variable specifies one vector to be used as the initial state around which an iterative algorithm starts. By default, this initial state is not required and is equal to the background $\mathbf{x}^b$ . Its value must allow to build a vector of the same size as the background. If provided, it replaces the background only for initialization.

Example : {"InitializationPoint":[1, 2, 3, 4, 5]}

MaximumNumberOfIterations

Integer value. This key indicates the maximum number of internal iterations allowed for iterative optimization. The default is 15000, which is very similar to no limit on iterations. It is then recommended to adapt this parameter to the needs on real problems. For some optimizers, the effective stopping step can be slightly different of the limit due to algorithm internal control requirements. One can refer to the section describing ways for Convergence control for calculation cases and iterative algorithms for more detailed recommendations.

Example: {"MaximumNumberOfIterations":100}

Minimizer: Predefined name. This key allows to choose the optimization minimizer. The default choice is “LBFGSB”, and the possible ones are “LBFGSB” (nonlinear constrained minimizer, see [Byrd95], [Morales11], [Zhu97]), “TNC” (nonlinear constrained minimizer), “CG” (nonlinear unconstrained minimizer), “BFGS” (nonlinear unconstrained minimizer), It is strongly recommended to stay with the default.

NumberOfSamplesForQuantiles

Integer value. This key indicates the number of simulation to be done in order to estimate the quantiles. This option is useful only if the supplementary calculation “SimulationQuantiles” has been chosen. The default is 100, which is often sufficient for correct estimation of common quantiles at 5%, 10%, 90% or 95%.

Example: {"NumberOfSamplesForQuantiles":100}

ProjectedGradientTolerance

Real value. This key indicates a limit value, leading to stop successfully the iterative optimization process when all the components of the projected gradient are under this limit. It is only used for constrained optimizers. The default is -1, that is the internal default of each minimizer (generally 1.e-5), and it is not recommended to change it.

Example: {"ProjectedGradientTolerance":-1}

Quantiles

List of real values. This list indicates the values of quantile, between 0 and 1, to be estimated by simulation around the optimal state. The sampling uses a multivariate Gaussian random sampling, directed by the a posteriori covariance matrix. This option is useful only if the supplementary calculation “SimulationQuantiles” has been chosen. The default is a void list.

Example: {"Quantiles":[0.1,0.9]}

SetSeed

Integer value. This key allow to give an integer in order to fix the seed of the random generator used in the algorithm. By default, the seed is left uninitialized, and so use the default initialization from the computer, which then change at each study. To ensure the reproducibility of results involving random samples, it is strongly advised to initialize the seed. A simple convenient value is for example 123456789. It is recommended to put an integer with more than 6 or 7 digits to properly initialize the random generator.

Example: {"SetSeed":123456789}

SimulationForQuantiles

Predefined name. This key indicates the type of simulation, linear (with the tangent observation operator applied to perturbation increments around the optimal state) or non-linear (with standard observation operator applied to perturbed states), one want to do for each perturbation. It changes mainly the time of each elementary calculation, usually longer in non-linear than in linear. This option is useful only if the supplementary calculation “SimulationQuantiles” has been chosen. The default value is “Linear”, and the possible choices are “Linear” and “NonLinear”.

Example: {"SimulationForQuantiles":"Linear"}

StateBoundsForQuantiles

List of pairs of real values. This key allows to define pairs of upper and lower bounds for every state variable used for quantile simulations. Bounds have to be given by a list of list of pairs of lower/upper bounds for each variable, with possibly None every time there is no bound.

If these bounds are not defined for quantile simulation and if optimization bounds are defined, they are used for quantile simulation. If these bounds for quantile simulation are defined, they are used regardless of the optimization bounds defined. If this variable is set to None, then no bounds are used for the states used in the quantile simulation regardless of the optimization bounds defined.

Example : {"StateBoundsForQuantiles":[[2.,5.],[1.e-2,10.],[-30.,None],[None,None]]}

StoreSupplementaryCalculations

List of names. This list indicates the names of the supplementary variables, that can be available during or at the end of the algorithm, if they are initially required by the user. Their availability involves, potentially, costly calculations or memory consumptions. The default is then a void list, none of these variables being calculated and stored by default (excepted the unconditional variables). The possible names are in the following list (the detailed description of each named variable is given in the following part of this specific algorithmic documentation, in the sub-section “Information and variables available at the end of the algorithm”): [ “Analysis”, “APosterioriCorrelations”, “APosterioriCovariance”, “APosterioriStandardDeviations”, “APosterioriVariances”, “BMA”, “CostFunctionJ”, “CostFunctionJAtCurrentOptimum”, “CostFunctionJb”, “CostFunctionJbAtCurrentOptimum”, “CostFunctionJo”, “CostFunctionJoAtCurrentOptimum”, “CurrentIterationNumber”, “CurrentOptimum”, “CurrentState”, “CurrentStepNumber”, “ForecastState”, “IndexOfOptimum”, “Innovation”, “InnovationAtCurrentAnalysis”, “InnovationAtCurrentState”, “JacobianMatrixAtBackground”, “JacobianMatrixAtOptimum”, “KalmanGainAtOptimum”, “MahalanobisConsistency”, “OMA”, “OMB”, “SampledStateForQuantiles”, “SigmaObs2”, “SimulatedObservationAtBackground”, “SimulatedObservationAtCurrentOptimum”, “SimulatedObservationAtCurrentState”, “SimulatedObservationAtOptimum”, “SimulationQuantiles”, ].

Example : {"StoreSupplementaryCalculations":["CurrentState", "Residu"]}

Variant

Predefined name. This key allows to choose one of the possible variants for the main algorithm. The default variant is the original “3DVAR”, and the possible choices are “3DVAR” (Classical 3D Variational analysis), “3DVAR-VAN” (3D Variational Analysis with No inversion of B), “3DVAR-Incr” (Incremental 3DVAR), “3DVAR-PSAS” (Physical-space Statistical Analysis Scheme for 3DVAR), It is highly recommended to keep the default value.

Example : {"Variant":"3DVAR"}

13.1.3. Information and variables available at the end of the algorithm¶

At the output, after executing the algorithm, there are information and variables originating from the calculation. The description of Variables and information available at the output show the way to obtain them by the method named get, of the variable “ADD” of the post-processing in graphical interface, or of the case in textual interface. The input variables, available to the user at the output in order to facilitate the writing of post-processing procedures, are described in the Inventory of potentially available information at the output.

Permanent outputs (non conditional)

The unconditional outputs of the algorithm are the following:

Analysis

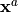List of vectors. Each element of this variable is an optimal state $\mathbf{x}^*$ in optimization, an interpolate or an analysis $\mathbf{x}^a$ in data assimilation.

Example: xa = ADD.get("Analysis")[-1]

CostFunctionJ

List of values. Each element is a value of the chosen error function $J$ .

Example: J = ADD.get("CostFunctionJ")[:]

CostFunctionJb

List of values. Each element is a value of the error function $J^b$ , that is of the background difference part. If this part does not exist in the error function, its value is zero.

Example: Jb = ADD.get("CostFunctionJb")[:]

CostFunctionJo

List of values. Each element is a value of the error function $J^o$ , that is of the observation difference part.

Example: Jo = ADD.get("CostFunctionJo")[:]

Set of on-demand outputs (conditional or not)

The whole set of algorithm outputs (conditional or not), sorted by alphabetical order, is the following:

Analysis

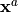List of vectors. Each element of this variable is an optimal state $\mathbf{x}^*$ in optimization, an interpolate or an analysis $\mathbf{x}^a$ in data assimilation.

Example: xa = ADD.get("Analysis")[-1]

APosterioriCorrelations

List of matrices. Each element is an a posteriori error correlations matrix of the optimal state, coming from the $\mathbf{A}$ covariance matrix. In order to get them, this a posteriori error covariances calculation has to be requested at the same time.

Example: apc = ADD.get("APosterioriCorrelations")[-1]

APosterioriCovariance

List of matrices. Each element is an a posteriori error covariance matrix $\mathbf{A}$ of the optimal state.

Example: apc = ADD.get("APosterioriCovariance")[-1]

APosterioriStandardDeviations

List of matrices. Each element is an a posteriori error standard errors diagonal matrix of the optimal state, coming from the $\mathbf{A}$ covariance matrix. In order to get them, this a posteriori error covariances calculation has to be requested at the same time.

Example: aps = ADD.get("APosterioriStandardDeviations")[-1]

APosterioriVariances

List of matrices. Each element is an a posteriori error variance errors diagonal matrix of the optimal state, coming from the $\mathbf{A}$ covariance matrix. In order to get them, this a posteriori error covariances calculation has to be requested at the same time.

Example: apv = ADD.get("APosterioriVariances")[-1]

BMA

List of vectors. Each element is a vector of difference between the background and the optimal state.

Example: bma = ADD.get("BMA")[-1]

CostFunctionJ

List of values. Each element is a value of the chosen error function $J$ .

Example: J = ADD.get("CostFunctionJ")[:]

CostFunctionJAtCurrentOptimum

List of values. Each element is a value of the error function $J$ . At each step, the value corresponds to the optimal state found from the beginning.

Example: JACO = ADD.get("CostFunctionJAtCurrentOptimum")[:]

CostFunctionJb

List of values. Each element is a value of the error function $J^b$ , that is of the background difference part. If this part does not exist in the error function, its value is zero.

Example: Jb = ADD.get("CostFunctionJb")[:]

CostFunctionJbAtCurrentOptimum

List of values. Each element is a value of the error function $J^b$ . At each step, the value corresponds to the optimal state found from the beginning. If this part does not exist in the error function, its value is zero.

Example: JbACO = ADD.get("CostFunctionJbAtCurrentOptimum")[:]

CostFunctionJo

List of values. Each element is a value of the error function $J^o$ , that is of the observation difference part.

Example: Jo = ADD.get("CostFunctionJo")[:]

CostFunctionJoAtCurrentOptimum

List of values. Each element is a value of the error function $J^o$ , that is of the observation difference part. At each step, the value corresponds to the optimal state found from the beginning.

Example: JoACO = ADD.get("CostFunctionJoAtCurrentOptimum")[:]

CurrentIterationNumber

List of integers. Each element is the iteration index at the current step during the iterative algorithm procedure. There is one iteration index value per assimilation step corresponding to an observed state.

Example: cin = ADD.get("CurrentIterationNumber")[-1]

CurrentOptimum

List of vectors. Each element is the optimal state obtained at the usual step of the iterative algorithm procedure of the optimization algorithm. It is not necessarily the last state.

Example: xo = ADD.get("CurrentOptimum")[:]

CurrentState

List of vectors. Each element is a usual state vector used during the iterative algorithm procedure.

Example: xs = ADD.get("CurrentState")[:]

CurrentStepNumber

List of integers. Each element is the index of the current step in the iterative process, driven by the series of observations, of the algorithm used. This corresponds to the observation step used. Note: it is not the index of the current iteration of the algorithm even if it coincides for non-iterative algorithms.

Example: csn = ADD.get("CurrentStepNumber")[-1]

ForecastState

List of vectors. Each element is a state vector forecasted by the model during the iterative algorithm procedure.

Example: xf = ADD.get("ForecastState")[:]

IndexOfOptimum

List of integers. Each element is the iteration index of the optimum obtained at the current step of the iterative algorithm procedure of the optimization algorithm. It is not necessarily the number of the last iteration.

Example: ioo = ADD.get("IndexOfOptimum")[-1]

Innovation

List of vectors. Each element is an innovation vector, which is in static the difference between the optimal and the background, and in dynamic the evolution increment.

Example: d = ADD.get("Innovation")[-1]

InnovationAtCurrentAnalysis

List of vectors. Each element is an innovation vector at current analysis. This quantity is identical to the innovation vector at analysed state in the case of a single-state assimilation.

Example: da = ADD.get("InnovationAtCurrentAnalysis")[-1]

InnovationAtCurrentState

List of vectors. Each element is an innovation vector at current state before analysis.

Example: ds = ADD.get("InnovationAtCurrentState")[-1]

JacobianMatrixAtBackground

List of matrices. Each element is the jacobian matrix of partial derivatives of the output of the observation operator with respect to the input parameters, one column of derivatives per parameter. It is calculated at the initial state.

Example: gradh = ADD.get("JacobianMatrixAtBackground")[-1]

JacobianMatrixAtOptimum

List of matrices. Each element is the jacobian matrix of partial derivatives of the output of the observation operator with respect to the input parameters, one column of derivatives per parameter. It is calculated at the optimal state.

Example: gradh = ADD.get("JacobianMatrixAtOptimum")[-1]

KalmanGainAtOptimum

List of matrices. Each element is a standard Kalman gain matrix, evaluated using the linearized observation operator. It is calculated at the optimal state.

Example: kg = ADD.get("KalmanGainAtOptimum")[-1]

MahalanobisConsistency

List of values. Each element is a value of the Mahalanobis quality indicator.

Example: mc = ADD.get("MahalanobisConsistency")[-1]

OMA

List of vectors. Each element is a vector of difference between the observation and the optimal state in the observation space.

Example: oma = ADD.get("OMA")[-1]

OMB

List of vectors. Each element is a vector of difference between the observation and the background state in the observation space.

Example: omb = ADD.get("OMB")[-1]

SampledStateForQuantiles

List of vector series. Each element is a series of column state vectors, generated to estimate by simulation and/or observation the quantile values required by the user. There are as many states as the number of samples required for this quantile estimate.

Example : xq = ADD.get("SampledStateForQuantiles")[:]

SigmaObs2

List of values. Each element is a value of the quality indicator $(\sigma^o)^2$ of the observation part.

Example: so2 = ADD.get("SigmaObs")[-1]

SimulatedObservationAtBackground

List of vectors. Each element is a vector of observation simulated by the observation operator from the background $\mathbf{x}^b$ . It is the forecast from the background, and it is sometimes called “Dry”.

Example: hxb = ADD.get("SimulatedObservationAtBackground")[-1]

SimulatedObservationAtCurrentOptimum

List of vectors. Each element is a vector of observation simulated from the optimal state obtained at the current step the optimization algorithm, that is, in the observation space.

Example: hxo = ADD.get("SimulatedObservationAtCurrentOptimum")[-1]

SimulatedObservationAtCurrentState

List of vectors. Each element is an observed vector simulated by the observation operator from the current state, that is, in the observation space.

Example: hxs = ADD.get("SimulatedObservationAtCurrentState")[-1]

SimulatedObservationAtOptimum

List of vectors. Each element is a vector of observation obtained by the observation operator from simulation on the analysis or optimal state 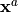$\mathbf{x}^a$ . It is the observed forecast from the analysis or the optimal state, and it is sometimes called “Forecast”.

Example: hxa = ADD.get("SimulatedObservationAtOptimum")[-1]

SimulationQuantiles

List of vector series. Each element is a series of observation column vectors, corresponding, for a particular quantile required by the user, to the observed state that achieves the requested quantile. Each observation column vector is rendered in the same order as the quantile values required by the user.

Example: sQuantiles = ADD.get("SimulationQuantiles")[:]

13.1.4. Python (TUI) use examples¶

Here is one or more very simple examples of the proposed algorithm and its parameters, written in [DocR] Textual User Interface for ADAO (TUI/API). Moreover, when it is possible, the information given as input also allows to define an equivalent case in [DocR] Graphical User Interface for ADAO (GUI/EFICAS).

13.1.4.1. First example¶

This example describes the calibration of parameters $\mathbf{x}$ of a quadratic observation model $H$ . This model $H$ is here represented as a function named QuadFunction for the purpose of this example. This function get as input the coefficients vector $\mathbf{x}$ of the quadratic form, and return as output the evaluation vector $\mathbf{y}$ of the quadratic model at the predefined internal control points, predefined in a static way in the model.

The calibration is done using an initial coefficient set (background state specified by Xb in the example), and with the information $\mathbf{y}^o$ (specified by Yobs in the example) of 5 measures obtained in these same internal control points. We set twin experiments (see To test a data assimilation chain: the twin experiments) and the measurements are supposed to be perfect. We choose to emphasize the observations, versus the background, by setting artificially a great variance for the background error, here of $10^{6}$ .

The adjustment is carried out by displaying intermediate results using “observer” (for reference, see Getting information on special variables during the ADAO calculation) during iterative optimization.

# -*- coding: utf-8 -*-
#
from numpy import array, ravel
def QuadFunction( coefficients ):
    """
    Quadratic simulation in x: y = a x^2 + b x + c
    """
    a, b, c  = list(ravel(coefficients))
    x_points = (-5, 0, 1, 3, 10)
    y_points = []
    for x in x_points:
        y_points.append( a*x*x + b*x + c )
    return array(y_points)
#
Xb   = array([1., 1., 1.])
Yobs = array([57, 2, 3, 17, 192])
#
print("Resolution of the calibration problem")
print("-------------------------------------")
print("")
from adao import adaoBuilder
case = adaoBuilder.New()
case.setBackground( Vector = Xb, Stored=True )
case.setBackgroundError( ScalarSparseMatrix = 1.e6 )
case.setObservation( Vector = Yobs, Stored=True )
case.setObservationError( ScalarSparseMatrix = 1. )
case.setObservationOperator( OneFunction = QuadFunction )
case.setAlgorithmParameters(
    Algorithm='3DVAR',
    Parameters={
        'MaximumNumberOfIterations': 100,
        'StoreSupplementaryCalculations': [
            'CurrentState',
            ],
        },
    )
case.setObserver(
    Info="  Intermediate state at the current iteration:",
    Template='ValuePrinter',
    Variable='CurrentState',
    )
case.execute()
print("")
#
#-------------------------------------------------------------------------------
#
print("Calibration of %i coefficients in a 1D quadratic function on %i measures"%(
    len(case.get('Background')),
    len(case.get('Observation')),
    ))
print("----------------------------------------------------------------------")
print("")
print("Observation vector.................:", ravel(case.get('Observation')))
print("A priori background state..........:", ravel(case.get('Background')))
print("")
print("Expected theoretical coefficients..:", ravel((2,-1,2)))
print("")
print("Number of iterations...............:", len(case.get('CurrentState')))
print("Number of simulations..............:", len(case.get('CurrentState'))*4)
print("Calibration resulting coefficients.:", ravel(case.get('Analysis')[-1]))
#
Xa = case.get('Analysis')[-1]
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10, 4)
#
plt.figure()
plt.plot((-5,0,1,3,10),QuadFunction(Xb),'b--',label="Simulation at background")
plt.plot((-5,0,1,3,10),Yobs,            'kX', label='Observation',markersize=10)
plt.plot((-5,0,1,3,10),QuadFunction(Xa),'r-', label="Simulation at optimum")
plt.legend()
plt.title('Coefficients calibration', fontweight='bold')
plt.xlabel('Arbitrary coordinate')
plt.ylabel('Observations')
plt.savefig("simple_3DVAR1.png")

The execution result is the following:

Resolution of the calibration problem
-------------------------------------

  Intermediate state at the current iteration: [1. 1. 1.]
  Intermediate state at the current iteration: [1.99739508 1.07086406 1.01346638]
  Intermediate state at the current iteration: [1.83891966 1.04815981 1.01208385]
  Intermediate state at the current iteration: [1.8390702  1.03667176 1.01284797]
  Intermediate state at the current iteration: [1.83967236 0.99071957 1.01590445]
  Intermediate state at the current iteration: [1.84208099 0.8069108  1.02813037]
  Intermediate state at the current iteration: [ 1.93711599 -0.56383145  1.12097995]
  Intermediate state at the current iteration: [ 1.99838848 -1.00480573  1.1563713 ]
  Intermediate state at the current iteration: [ 2.0135905  -1.04815933  1.16155285]
  Intermediate state at the current iteration: [ 2.01385679 -1.03874809  1.16129657]
  Intermediate state at the current iteration: [ 2.01377856 -1.03700044  1.16157611]
  Intermediate state at the current iteration: [ 2.01338902 -1.02943736  1.16528951]
  Intermediate state at the current iteration: [ 2.01265633 -1.0170847   1.17793974]
  Intermediate state at the current iteration: [ 2.0112487  -0.99745509  1.21485091]
  Intermediate state at the current iteration: [ 2.00863696 -0.96943284  1.30917045]
  Intermediate state at the current iteration: [ 2.00453385 -0.94011716  1.51021882]
  Intermediate state at the current iteration: [ 2.00013539 -0.93313893  1.80539433]
  Intermediate state at the current iteration: [ 1.95437244 -0.76890418  2.04566856]
  Intermediate state at the current iteration: [ 1.99797362 -0.92538074  1.81674451]
  Intermediate state at the current iteration: [ 1.99760514 -0.95929669  2.01402091]
  Intermediate state at the current iteration: [ 1.99917565 -0.99152672  2.03171791]
  Intermediate state at the current iteration: [ 1.99990376 -0.99963123  2.00671578]
  Intermediate state at the current iteration: [ 1.99999841 -1.00005285  2.00039699]
  Intermediate state at the current iteration: [ 2.00000014 -1.00000307  2.00000221]
  Intermediate state at the current iteration: [ 2.         -0.99999992  1.99999987]

Calibration of 3 coefficients in a 1D quadratic function on 5 measures
----------------------------------------------------------------------

Observation vector.................: [ 57.   2.   3.  17. 192.]
A priori background state..........: [1. 1. 1.]

Expected theoretical coefficients..: [ 2 -1  2]

Number of iterations...............: 25
Number of simulations..............: 100
Calibration resulting coefficients.: [ 2.         -0.99999992  1.99999987]

The figures illustrating the result of its execution are as follows:

In the figure, the lines simply join the simulated values at the control points and make them easier to read.

We see, in this particularly simple case, that the optimum is identical to the values of coefficients [2, -1, 2] used to generate the pseudo-observations for the twin experiment. Naturally, the final simulation obtained with the adjusted coefficients coincides with the observations at the 5 control points.

To illustrate more clearly the recalibration performed, using the same information, we can plot the “continuous” version of the quadratic curves available for the background state of the coefficients, and for the optimal state of the coefficients, together with the values obtained at the control points. In addition, to improve readability, the lines joining the simulations in the previous graph have been removed.

13.1.4.2. Second example¶

The 3DVAR can also be used for a time analysis of the observations of a given dynamic model. In this case, the analysis is performed iteratively, at the arrival of each observation. For this example, we use the same simple dynamic system [Welch06] that is analyzed in the Kalman Filter Python (TUI) use examples. For a good understanding of time management, please refer to the Timeline of steps for data assimilation operators in dynamics and the explanations in the section Going further in data assimilation for dynamics.

At each step, the classical 3DVAR analysis updates only the state of the system. By modifying the a priori covariance values with respect to the initial assumptions of the filtering, this 3DVAR reanalysis allows to converge towards the true trajectory, as illustrated in the associated figure, in a slightly slower speed than with a Kalman Filter.

Note

Note about a posteriori covariances: classically, the 3DVAR iterative analysis updates only the state and not its covariance. As the assumptions of operators and a priori covariance remain unchanged here during the evolution, the a posteriori covariance is constant. The following plot of this a posteriori covariance allows us to insist on this property, which is entirely expected from the 3DVAR analysis. A more advanced hypothesis is proposed in the forthcoming example.

# -*- coding: utf-8 -*-
#
from numpy import array, random
random.seed(1234567)
Xtrue = -0.37727
Yobs = []
for i in range(51):
    Yobs.append([random.normal(Xtrue, 0.1, size=(1,)),])
#
print("Variational estimation of a time trajectory")
print("-------------------------------------------")
print("  Noisy measurements acquired on %i time steps"%(len(Yobs)-1,))
print("")
from adao import adaoBuilder
case = adaoBuilder.New()
#
case.setBackground         (Vector             = [0.])
case.setBackgroundError    (ScalarSparseMatrix = 0.1**2)
#
case.setObservationOperator(Matrix             = [1.])
case.setObservation        (VectorSerie        = Yobs)
case.setObservationError   (ScalarSparseMatrix = 0.3**2)
#
case.setEvolutionModel     (Matrix             = [1.])
case.setEvolutionError     (ScalarSparseMatrix = 1e-5)
#
case.setAlgorithmParameters(
    Algorithm="3DVAR",
    Parameters={
        "EstimationOf":"State",
        "StoreSupplementaryCalculations":[
            "Analysis",
            "APosterioriCovariance",
            ],
        },
    )
#
case.execute()
Xa = case.get("Analysis")
Pa = case.get("APosterioriCovariance")
#
print("  Analyzed state at final observation:", Xa[-1])
print("")
print("  Final a posteriori variance:", Pa[-1])
print("")
#
#-------------------------------------------------------------------------------
#
Observations = array([yo[0]   for yo in Yobs])
Estimates    = array([xa[0]   for xa in case.get("Analysis")])
Variances    = array([pa[0,0] for pa in case.get("APosterioriCovariance")])
#
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10, 4)
#
plt.figure()
plt.plot(Observations,'kx',label='Noisy measurements')
plt.plot(Estimates,'r-',label='Estimated state')
plt.axhline(Xtrue,color='b',label='Truth value')
plt.legend()
plt.title('Estimate of the state', fontweight='bold')
plt.xlabel('Observation step')
plt.ylabel('Voltage')
plt.savefig("simple_3DVAR2_state.png")
#
plt.figure()
iobs = range(1,len(Observations))
plt.plot(iobs,Variances[iobs],label='A posteriori error variance')
plt.title('Estimate of the a posteriori error variance', fontweight='bold')
plt.xlabel('Observation step')
plt.ylabel('$(Voltage)^2$')
plt.setp(plt.gca(),'ylim',[0,.01])
plt.savefig("simple_3DVAR2_variance.png")

The execution result is the following:

Variational estimation of a time trajectory
-------------------------------------------
  Noisy measurements acquired on 50 time steps

  Analyzed state at final observation: [-0.37110687]

  Final a posteriori variance: [[0.009]]

The figures illustrating the result of its execution are as follows:

13.1.4.3. Third example¶

From the preceding example, if one wants to adapt the time convergence of the 3DVAR, one can change, for example, the a priori covariance assumptions of the background errors during the iterations. This update is an assumption of the user, and there are multiple alternatives that will depend on the physics of the case. We illustrate one of them here.

We choose, in an arbitrary way, to make the a priori covariance of the background errors to decrease by a constant factor $0.9^2=0.81$ as long as it remains above a limit value of $0.1^2=0.01$ (which is the fixed value of a priori covariance of the background errors of the previous example), knowing that it starts at the value 1 (which is the fixed value of a priori covariance of the background errors used for the first step of Kalman filtering). This value is updated at each step, by re-injecting it as the a priori covariance of the state which is used as a background in the next step of analysis, in an explicit loop.

We notice in this case that the state estimation converges faster to the true value, and that the assimilation then behaves similarly to the examples for the Kalman Filter, or to the previous example with the manually adapted a priori covariances. Moreover, the a posteriori covariance decreases as long as we force the decrease of the a priori covariance.

Note

We insist on the fact that the a priori covariance variations, which determine the a posteriori covariance variations, are a user arbitrary assumption and not an obligation. This assumption must therefore be adapted to the physical case.

# -*- coding: utf-8 -*-
#
from numpy import array, random
random.seed(1234567)
Xtrue = -0.37727
Yobs = []
for i in range(51):
    Yobs.append([random.normal(Xtrue, 0.1, size=(1,)),])
#
print("Variational estimation of a time trajectory")
print("-------------------------------------------")
print("  Noisy measurements acquired on %i time steps"%(len(Yobs)-1,))
print("")
from adao import adaoBuilder
case = adaoBuilder.New()
#
case.setBackground         (Vector             = [0.])
#
case.setObservationOperator(Matrix             = [1.])
case.setObservationError   (ScalarSparseMatrix = 0.3**2)
#
case.setEvolutionModel     (Matrix             = [1.])
case.setEvolutionError     (ScalarSparseMatrix = 1e-5)
#
case.setAlgorithmParameters(
    Algorithm="3DVAR",
    Parameters={
        "EstimationOf":"State",
        "StoreSupplementaryCalculations":[
            "Analysis",
            "APosterioriCovariance",
            ],
        },
    )
#
# Loop to obtain an analysis at each observation arrival
#
Ca = 1.
for i in range(1,len(Yobs)):
    case.setObservation(Vector = Yobs[i])
    case.setBackgroundError(ScalarSparseMatrix = Ca) # Update of the covariance
    case.execute( nextStep = True )
    #
    # Hypothesis of the a priori covariance decay of the background error
    #
    if float(Ca) <= 0.1**2:
        Ca = 0.1**2
    else:
        Ca = Ca * 0.9**2
#
Xa = case.get("Analysis")
Pa = case.get("APosterioriCovariance")
#
print("  Analyzed state at final observation:", Xa[-1])
print("")
print("  Final a posteriori variance:", Pa[-1])
print("")
#
#-------------------------------------------------------------------------------
#
Observations = array([yo[0]   for yo in Yobs])
Estimates    = array([xa[0]   for xa in case.get("Analysis")])
Variances    = array([pa[0,0] for pa in case.get("APosterioriCovariance")])
#
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10, 4)
#
plt.figure()
plt.plot(Observations,'kx',label='Noisy measurements')
plt.plot(Estimates,'r-',label='Estimated state')
plt.axhline(Xtrue,color='b',label='Truth value')
plt.legend()
plt.title('Estimate of the state', fontweight='bold')
plt.xlabel('Observation step')
plt.ylabel('Voltage')
plt.savefig("simple_3DVAR3_state.png")
#
plt.figure()
iobs = range(1,len(Observations))
plt.plot(iobs,Variances[iobs],label='A posteriori error variance')
plt.title('Estimate of the a posteriori error variance', fontweight='bold')
plt.xlabel('Observation step')
plt.ylabel('$(Voltage)^2$')
plt.savefig("simple_3DVAR3_variance.png")

The execution result is the following:

Variational estimation of a time trajectory
-------------------------------------------
  Noisy measurements acquired on 50 time steps

  Analyzed state at final observation: [-0.37334336]

  Final a posteriori variance: [[0.009]]

The figures illustrating the result of its execution are as follows:

13.1.5. See also¶

References to other sections:

Bibliographical references: