13.5. Calculation algorithm “DifferentialEvolution”

13.5.1. Description

This algorithm realizes an estimation of the state of a system by minimization of a cost function J by using an evolutionary strategy of differential evolution. It is a method that does not use the derivatives of the cost function. It falls in the same category than the Calculation algorithm “DerivativeFreeOptimization”, the Calculation algorithm “ParticleSwarmOptimization” or the Calculation algorithm “TabuSearch”.

This is an optimization method allowing for global minimum search of a general error function J of type L^1, L^2 or L^{\infty}, with or without weights. The default error function is the augmented weighted least squares function, classically used in data assimilation.

13.5.2. Optional and required commands

The general required commands, available in the editing user graphical or textual interface, are the following:

Background

Vector. The variable indicates the background or initial vector used, previously noted as \mathbf{x}^b. Its value is defined as a “Vector” or “VectorSerie” type object. Its availability in output is conditioned by the boolean “Stored” associated with input.

BackgroundError

Matrix. This indicates the background error covariance matrix, previously noted as \mathbf{B}. Its value is defined as a “Matrix” type object, a “ScalarSparseMatrix” type object, or a “DiagonalSparseMatrix” type object, as described in detail in the section Requirements to describe covariance matrices. Its availability in output is conditioned by the boolean “Stored” associated with input.

Observation

List of vectors. The variable indicates the observation vector used for data assimilation or optimization, and usually noted \mathbf{y}^o. Its value is defined as an object of type “Vector” if it is a single observation (temporal or not) or “VectorSeries” if it is a succession of observations. Its availability in output is conditioned by the boolean “Stored” associated in input.

ObservationError

Matrix. The variable indicates the observation error covariance matrix, usually noted as 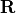\mathbf{R}. It is defined as a “Matrix” type object, a “ScalarSparseMatrix” type object, or a “DiagonalSparseMatrix” type object, as described in detail in the section Requirements to describe covariance matrices. Its availability in output is conditioned by the boolean “Stored” associated with input.

ObservationOperator

Operator. The variable indicates the observation operator, usually noted as H, which transforms the input parameters \mathbf{x} to results \mathbf{y} to be compared to observations \mathbf{y}^o. Its value is defined as a “Function” type object or a “Matrix” type one. In the case of “Function” type, different functional forms can be used, as described in the section Requirements for functions describing an operator. If there is some control U included in the observation, the operator has to be applied to a pair (X,U).

The general optional commands, available in the editing user graphical or textual interface, are indicated in List of commands and keywords for data assimilation or optimization case. Moreover, the parameters of the command “AlgorithmParameters” allows to choose the specific options, described hereafter, of the algorithm. See Description of options of an algorithm by “AlgorithmParameters” for the good use of this command.

The options are the following:

Minimizer

Predefined name. This key allows to choose the optimization strategy for the minimizer. The default choice is “BEST1BIN”, and the possible ones, among the multiples crossover and mutation strategies, are “BEST1BIN”, “BEST1EXP”, “BEST2BIN”, “BEST2EXP”, “RAND1BIN”, “RAND1EXP”, “RAND2BIN”, “RAND2EXP”, “RANDTOBEST1BIN”, “RANDTOBEST1EXP”. It is highly recommended to keep the default value.

Example: {"Minimizer":"BEST1BIN"}

Bounds

List of pairs of real values. This key allows to define pairs of upper and lower bounds for every state variable being optimized. Bounds have to be given by a list of list of pairs of lower/upper bounds for each variable, with extreme values every time there is no bound (None is not allowed when there is no bound).

Example: {"Bounds":[[2.,5.],[1.e-2,10.],[-30.,1.e99],[-1.e99,1.e99]]}

CrossOverProbability_CR

Real value. This key is used to define the probability of recombination or crossover during the differential evolution. This variable is usually noted as CR in the literature, and it is required to be between 0 and 1. The default value is 0.7, and it is recommended to change it if necessary.

Example: {"CrossOverProbability_CR":0.7}

MaximumNumberOfIterations

Integer value. This key indicates the maximum number of internal iterations allowed for iterative optimization. The default is 15000, which is very similar to no limit on iterations. It is then recommended to adapt this parameter to the needs on real problems. For some optimizers, the effective stopping step can be slightly different of the limit due to algorithm internal control requirements. One can refer to the section describing ways for Convergence control for calculation cases and iterative algorithms for more detailed recommendations.

Example: {"MaximumNumberOfIterations":100}

MaximumNumberOfFunctionEvaluations

Integer value. This key indicates the maximum number of evaluation of the cost function to be optimized. The default is 15000, which is an arbitrary limit. It is then recommended to adapt this parameter to the needs on real problems. For some optimizers, the effective number of function evaluations can be slightly different of the limit due to algorithm internal control requirements.

Example: {"MaximumNumberOfFunctionEvaluations":50}

MutationDifferentialWeight_F

Pair of real values. This key is used to define the differential weight in the mutation step. This variable is usually noted as F in the literature. It can be constant if it is in the form of a single value, or randomly variable in the two given bounds in the pair. The default value is (0.5, 1).

Example: {"MutationDifferentialWeight_F":(0.5, 1)}

PopulationSize

Integer value. This key is used to define the (approximate) size of the population at each generation. This size is slightly adjusted to take into account the number of state variables to be optimized. The default value is 100, and it is recommended to choose a population between 1 and about ten times the number of state variables, the size being proportionally smaller as the number of variables increases.

Example: {"PopulationSize":100}

QualityCriterion

Predefined name. This key indicates the quality criterion, minimized to find the optimal state estimate. The default is the usual data assimilation criterion named “DA”, the augmented weighted least squares. The possible criterion has to be in the following list, where the equivalent names are indicated by the sign “<=>”: [“AugmentedWeightedLeastSquares” <=> “AWLS” <=> “DA”, “WeightedLeastSquares” <=> “WLS”, “LeastSquares” <=> “LS” <=> “L2”, “AbsoluteValue” <=> “L1”, “MaximumError” <=> “ME” <=> “Linf”]. See the section for Going further in the state estimation by optimization methods to have a detailed definition of these quality criteria.

Example: {"QualityCriterion":"DA"}

SetSeed

Integer value. This key allow to give an integer in order to fix the seed of the random generator used in the algorithm. By default, the seed is left uninitialized, and so use the default initialization from the computer, which then change at each study. To ensure the reproducibility of results involving random samples, it is strongly advised to initialize the seed. A simple convenient value is for example 123456789. It is recommended to put an integer with more than 6 or 7 digits to properly initialize the random generator.

Example: {"SetSeed":123456789}

StoreSupplementaryCalculations

List of names. This list indicates the names of the supplementary variables, that can be available during or at the end of the algorithm, if they are initially required by the user. Their availability involves, potentially, costly calculations or memory consumptions. The default is then a void list, none of these variables being calculated and stored by default (excepted the unconditional variables). The possible names are in the following list (the detailed description of each named variable is given in the following part of this specific algorithmic documentation, in the sub-section “Information and variables available at the end of the algorithm”): [ “Analysis”, “BMA”, “CostFunctionJ”, “CostFunctionJb”, “CostFunctionJo”, “CostFunctionJAtCurrentOptimum”, “CostFunctionJbAtCurrentOptimum”, “CostFunctionJoAtCurrentOptimum”, “CurrentIterationNumber”, “CurrentOptimum”, “CurrentState”, “IndexOfOptimum”, “Innovation”, “InnovationAtCurrentState”, “OMA”, “OMB”, “SimulatedObservationAtBackground”, “SimulatedObservationAtCurrentOptimum”, “SimulatedObservationAtCurrentState”, “SimulatedObservationAtOptimum”, ].

Example : {"StoreSupplementaryCalculations":["CurrentState", "Residu"]}

13.5.3. Information and variables available at the end of the algorithm

At the output, after executing the algorithm, there are information and variables originating from the calculation. The description of Variables and information available at the output show the way to obtain them by the method named get, of the variable “ADD” of the post-processing in graphical interface, or of the case in textual interface. The input variables, available to the user at the output in order to facilitate the writing of post-processing procedures, are described in the Inventory of potentially available information at the output.

Permanent outputs (non conditional)

The unconditional outputs of the algorithm are the following:

Analysis

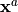List of vectors. Each element of this variable is an optimal state \mathbf{x}^* in optimization, an interpolate or an analysis \mathbf{x}^a in data assimilation.

Example: xa = ADD.get("Analysis")[-1]

CostFunctionJ

List of values. Each element is a value of the chosen error function J.

Example: J = ADD.get("CostFunctionJ")[:]

CostFunctionJb

List of values. Each element is a value of the error function J^b, that is of the background difference part. If this part does not exist in the error function, its value is zero.

Example: Jb = ADD.get("CostFunctionJb")[:]

CostFunctionJo

List of values. Each element is a value of the error function J^o, that is of the observation difference part.

Example: Jo = ADD.get("CostFunctionJo")[:]

CurrentState

List of vectors. Each element is a usual state vector used during the iterative algorithm procedure.

Example: xs = ADD.get("CurrentState")[:]

Set of on-demand outputs (conditional or not)

The whole set of algorithm outputs (conditional or not), sorted by alphabetical order, is the following:

Analysis

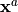List of vectors. Each element of this variable is an optimal state \mathbf{x}^* in optimization, an interpolate or an analysis \mathbf{x}^a in data assimilation.

Example: xa = ADD.get("Analysis")[-1]

BMA

List of vectors. Each element is a vector of difference between the background and the optimal state.

Example: bma = ADD.get("BMA")[-1]

CostFunctionJ

List of values. Each element is a value of the chosen error function J.

Example: J = ADD.get("CostFunctionJ")[:]

CostFunctionJb

List of values. Each element is a value of the error function J^b, that is of the background difference part. If this part does not exist in the error function, its value is zero.

Example: Jb = ADD.get("CostFunctionJb")[:]

CostFunctionJo

List of values. Each element is a value of the error function J^o, that is of the observation difference part.

Example: Jo = ADD.get("CostFunctionJo")[:]

CostFunctionJAtCurrentOptimum

List of values. Each element is a value of the error function J. At each step, the value corresponds to the optimal state found from the beginning.

Example: JACO = ADD.get("CostFunctionJAtCurrentOptimum")[:]

CostFunctionJbAtCurrentOptimum

List of values. Each element is a value of the error function J^b. At each step, the value corresponds to the optimal state found from the beginning. If this part does not exist in the error function, its value is zero.

Example: JbACO = ADD.get("CostFunctionJbAtCurrentOptimum")[:]

CostFunctionJoAtCurrentOptimum

List of values. Each element is a value of the error function J^o, that is of the observation difference part. At each step, the value corresponds to the optimal state found from the beginning.

Example: JoACO = ADD.get("CostFunctionJoAtCurrentOptimum")[:]

CurrentIterationNumber

List of integers. Each element is the iteration index at the current step during the iterative algorithm procedure. There is one iteration index value per assimilation step corresponding to an observed state.

Example: cin = ADD.get("CurrentIterationNumber")[-1]

CurrentOptimum

List of vectors. Each element is the optimal state obtained at the usual step of the iterative algorithm procedure of the optimization algorithm. It is not necessarily the last state.

Example: xo = ADD.get("CurrentOptimum")[:]

CurrentState

List of vectors. Each element is a usual state vector used during the iterative algorithm procedure.

Example: xs = ADD.get("CurrentState")[:]

IndexOfOptimum

List of integers. Each element is the iteration index of the optimum obtained at the current step of the iterative algorithm procedure of the optimization algorithm. It is not necessarily the number of the last iteration.

Example: ioo = ADD.get("IndexOfOptimum")[-1]

Innovation

List of vectors. Each element is an innovation vector, which is in static the difference between the optimal and the background, and in dynamic the evolution increment.

Example: d = ADD.get("Innovation")[-1]

InnovationAtCurrentState

List of vectors. Each element is an innovation vector at current state before analysis.

Example: ds = ADD.get("InnovationAtCurrentState")[-1]

OMA

List of vectors. Each element is a vector of difference between the observation and the optimal state in the observation space.

Example: oma = ADD.get("OMA")[-1]

OMB

List of vectors. Each element is a vector of difference between the observation and the background state in the observation space.

Example: omb = ADD.get("OMB")[-1]

SimulatedObservationAtBackground

List of vectors. Each element is a vector of observation simulated by the observation operator from the background \mathbf{x}^b. It is the forecast from the background, and it is sometimes called “Dry”.

Example: hxb = ADD.get("SimulatedObservationAtBackground")[-1]

SimulatedObservationAtCurrentOptimum

List of vectors. Each element is a vector of observation simulated from the optimal state obtained at the current step the optimization algorithm, that is, in the observation space.

Example: hxo = ADD.get("SimulatedObservationAtCurrentOptimum")[-1]

SimulatedObservationAtCurrentState

List of vectors. Each element is an observed vector simulated by the observation operator from the current state, that is, in the observation space.

Example: hxs = ADD.get("SimulatedObservationAtCurrentState")[-1]

SimulatedObservationAtOptimum

List of vectors. Each element is a vector of observation obtained by the observation operator from simulation on the analysis or optimal state 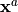\mathbf{x}^a. It is the observed forecast from the analysis or the optimal state, and it is sometimes called “Forecast”.

Example: hxa = ADD.get("SimulatedObservationAtOptimum")[-1]