13.16. Calculation algorithm “UnscentedKalmanFilter”¶
13.16.1. Description¶
This algorithm realizes an estimation of the state of a dynamic system by a “unscented” Kalman Filter, avoiding to have to perform the tangent and adjoint operators for the observation and evolution operators, as in the simple or extended Kalman filter.
It applies to non-linear observation and incremental evolution (process) operators with excellent robustness and performance qualities. It can be compared to the Calculation algorithm “EnsembleKalmanFilter”, whose qualities are similar for non-linear systems.
We notice that there is no analysis performed at the initial time step (numbered 0 in the time indexing) because there is no forecast at this time (the background is stored as a pseudo analysis at the initial time step). If the observations are provided in series by the user, the first one is therefore not used. For a good understanding of time management, please refer to the Timeline of steps for data assimilation operators in dynamics and the explanations in the section Going further in data assimilation for dynamics.
In case of linear of “slightly” non-linear operators, one can easily use the Calculation algorithm “ExtendedKalmanFilter” or even the Calculation algorithm “KalmanFilter”, which are often far less expensive to evaluate on small systems. One can verify the linearity of the operators with the help of the Checking algorithm “LinearityTest”.
A difference is made between the “unscented” Kalman filter taking into account bounds on the states (the variant named “2UKF”, which is recommended and used by default), and the canonical “unscented” Kalman filter conducted without any constraint (the variant named “UKF”, which is not recommended).
13.16.2. Optional and required commands¶
The general required commands, available in the editing user graphical or textual interface, are the following:
- Background
Vector. The variable indicates the background or initial vector used, previously noted as
 . Its value is defined as a
“Vector” or “VectorSerie” type object. Its availability in output is
conditioned by the boolean “Stored” associated with input.
. Its value is defined as a
“Vector” or “VectorSerie” type object. Its availability in output is
conditioned by the boolean “Stored” associated with input.
- BackgroundError
Matrix. This indicates the background error covariance matrix, previously noted as
 . Its value is defined as a “Matrix” type
object, a “ScalarSparseMatrix” type object, or a “DiagonalSparseMatrix”
type object, as described in detail in the section
Requirements to describe covariance matrices. Its availability in output is
conditioned by the boolean “Stored” associated with input.
. Its value is defined as a “Matrix” type
object, a “ScalarSparseMatrix” type object, or a “DiagonalSparseMatrix”
type object, as described in detail in the section
Requirements to describe covariance matrices. Its availability in output is
conditioned by the boolean “Stored” associated with input.
- EvolutionError
Matrix. The variable indicates the evolution error covariance matrix, usually noted as
 . It is defined as a “Matrix” type
object, a “ScalarSparseMatrix” type object, or a “DiagonalSparseMatrix”
type object, as described in detail in the section
Requirements to describe covariance matrices. Its availability in output is
conditioned by the boolean “Stored” associated with input.
. It is defined as a “Matrix” type
object, a “ScalarSparseMatrix” type object, or a “DiagonalSparseMatrix”
type object, as described in detail in the section
Requirements to describe covariance matrices. Its availability in output is
conditioned by the boolean “Stored” associated with input.
- EvolutionModel
Operator. The variable indicates the evolution model operator, usually noted
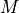 , which describes an elementary step of evolution. Its value
is defined as a “Function” type object or a “Matrix” type one. In the
case of “Function” type, different functional forms can be used, as
described in the section Requirements for functions describing an operator. If there
is some control
, which describes an elementary step of evolution. Its value
is defined as a “Function” type object or a “Matrix” type one. In the
case of “Function” type, different functional forms can be used, as
described in the section Requirements for functions describing an operator. If there
is some control  included in the evolution model, the operator has
to be applied to a pair
included in the evolution model, the operator has
to be applied to a pair  .
.
- Observation
List of vectors. The variable indicates the observation vector used for data assimilation or optimization, and usually noted
 .
Its value is defined as an object of type “Vector” if it is a single
observation (temporal or not) or “VectorSeries” if it is a succession of
observations. Its availability in output is conditioned by the boolean
“Stored” associated in input.
.
Its value is defined as an object of type “Vector” if it is a single
observation (temporal or not) or “VectorSeries” if it is a succession of
observations. Its availability in output is conditioned by the boolean
“Stored” associated in input.
- ObservationError
Matrix. The variable indicates the observation error covariance matrix, usually noted as
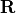 . It is defined as a “Matrix” type
object, a “ScalarSparseMatrix” type object, or a “DiagonalSparseMatrix”
type object, as described in detail in the section
Requirements to describe covariance matrices. Its availability in output is
conditioned by the boolean “Stored” associated with input.
. It is defined as a “Matrix” type
object, a “ScalarSparseMatrix” type object, or a “DiagonalSparseMatrix”
type object, as described in detail in the section
Requirements to describe covariance matrices. Its availability in output is
conditioned by the boolean “Stored” associated with input.
- ObservationOperator
Operator. The variable indicates the observation operator, usually noted as
 , which transforms the input parameters
, which transforms the input parameters  to
results
to
results  to be compared to observations
to be compared to observations
 . Its value is defined as a “Function” type object or a
“Matrix” type one. In the case of “Function” type, different functional
forms can be used, as described in the section
Requirements for functions describing an operator. If there is some control
. Its value is defined as a “Function” type object or a
“Matrix” type one. In the case of “Function” type, different functional
forms can be used, as described in the section
Requirements for functions describing an operator. If there is some control  included in the observation, the operator has to be applied to a pair
included in the observation, the operator has to be applied to a pair
 .
.
The general optional commands, available in the editing user graphical or textual interface, are indicated in List of commands and keywords for data assimilation or optimization case. Moreover, the parameters of the command “AlgorithmParameters” allows to choose the specific options, described hereafter, of the algorithm. See Description of options of an algorithm by “AlgorithmParameters” for the good use of this command.
The options are the following:
- Bounds
List of pairs of real values. This key allows to define pairs of upper and lower bounds for every state variable being optimized. Bounds have to be given by a list of list of pairs of lower/upper bounds for each variable, with a value of
Noneeach time there is no bound. The bounds can always be specified, but they are taken into account only by the constrained optimizers.Example:
{"Bounds":[[2.,5.],[1.e-2,10.],[-30.,None],[None,None]]}
- ConstrainedBy
Predefined name. This key allows to choose the method to take into account the bounds constraints. The only one available is the “EstimateProjection”, which projects the current state estimate on the bounds constraints.
Example:
{"ConstrainedBy":"EstimateProjection"}
- EstimationOf
Predefined name. This key allows to choose the type of estimation to be performed. It can be either state-estimation, with a value of “State”, or parameter-estimation, with a value of “Parameters”. The default choice is “State”.
Example:
{"EstimationOf":"Parameters"}
- Alpha, Beta, Kappa, Reconditioner
Real or integer values. These keys are internal scaling parameters. “Alpha” requires a value between 1.e-4 and 1. “Beta” has an optimal value of 2 for Gaussian a priori distribution. “Kappa” requires an integer value, and the right default is obtained by setting it to 0. “Reconditioner” requires a value between 1.e-3 and 10, it defaults to 1.
Example :
{"Alpha":1,"Beta":2,"Kappa":0,"Reconditioner":1}- StoreSupplementaryCalculations
List of names. This list indicates the names of the supplementary variables, that can be available during or at the end of the algorithm, if they are initially required by the user. Their availability involves, potentially, costly calculations or memory consumptions. The default is then a void list, none of these variables being calculated and stored by default (excepted the unconditional variables). The possible names are in the following list (the detailed description of each named variable is given in the following part of this specific algorithmic documentation, in the sub-section “Information and variables available at the end of the algorithm”): [ “Analysis”, “APosterioriCorrelations”, “APosterioriCovariance”, “APosterioriStandardDeviations”, “APosterioriVariances”, “BMA”, “CostFunctionJ”, “CostFunctionJAtCurrentOptimum”, “CostFunctionJb”, “CostFunctionJbAtCurrentOptimum”, “CostFunctionJo”, “CostFunctionJoAtCurrentOptimum”, “CurrentOptimum”, “CurrentState”, “ForecastCovariance”, “ForecastState”, “IndexOfOptimum”, “InnovationAtCurrentAnalysis”, “InnovationAtCurrentState”, “SimulatedObservationAtCurrentAnalysis”, “SimulatedObservationAtCurrentOptimum”, “SimulatedObservationAtCurrentState”, ].
Example :
{"StoreSupplementaryCalculations":["CurrentState", "Residu"]}
- Variant
Predefined name. This key allows to choose one of the possible variants for the main algorithm. The default variant is the constrained version “2UKF” of the original algorithm “UKF”, and the possible choices are “UKF” (Unscented Kalman Filter), “2UKF” (Constrained Unscented Kalman Filter). It is highly recommended to keep the default value.
Example :
{"Variant":"2UKF"}
13.16.3. Information and variables available at the end of the algorithm¶
At the output, after executing the algorithm, there are information and
variables originating from the calculation. The description of
Variables and information available at the output show the way to obtain them by the method
named get, of the variable “ADD” of the post-processing in graphical
interface, or of the case in textual interface. The input variables, available
to the user at the output in order to facilitate the writing of post-processing
procedures, are described in the Inventory of potentially available information at the output.
Permanent outputs (non conditional)
The unconditional outputs of the algorithm are the following:
- Analysis
List of vectors. Each element of this variable is an optimal state
 in optimization, an interpolate or an analysis
in optimization, an interpolate or an analysis
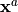 in data assimilation.
in data assimilation.Example:
xa = ADD.get("Analysis")[-1]
Set of on-demand outputs (conditional or not)
The whole set of algorithm outputs (conditional or not), sorted by alphabetical order, is the following:
- Analysis
List of vectors. Each element of this variable is an optimal state
 in optimization, an interpolate or an analysis
in optimization, an interpolate or an analysis
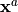 in data assimilation.
in data assimilation.Example:
xa = ADD.get("Analysis")[-1]
- APosterioriCorrelations
List of matrices. Each element is an a posteriori error correlations matrix of the optimal state, coming from the
 covariance
matrix. In order to get them, this a posteriori error covariances
calculation has to be requested at the same time.
covariance
matrix. In order to get them, this a posteriori error covariances
calculation has to be requested at the same time.Example:
apc = ADD.get("APosterioriCorrelations")[-1]
- APosterioriCovariance
List of matrices. Each element is an a posteriori error covariance matrix
 of the optimal state.
of the optimal state.Example:
apc = ADD.get("APosterioriCovariance")[-1]
- APosterioriStandardDeviations
List of matrices. Each element is an a posteriori error standard errors diagonal matrix of the optimal state, coming from the
 covariance matrix. In order to get them, this a posteriori error
covariances calculation has to be requested at the same time.
covariance matrix. In order to get them, this a posteriori error
covariances calculation has to be requested at the same time.Example:
aps = ADD.get("APosterioriStandardDeviations")[-1]
- APosterioriVariances
List of matrices. Each element is an a posteriori error variance errors diagonal matrix of the optimal state, coming from the
 covariance matrix. In order to get them, this a posteriori error
covariances calculation has to be requested at the same time.
covariance matrix. In order to get them, this a posteriori error
covariances calculation has to be requested at the same time.Example:
apv = ADD.get("APosterioriVariances")[-1]
- BMA
List of vectors. Each element is a vector of difference between the background and the optimal state.
Example:
bma = ADD.get("BMA")[-1]
- CostFunctionJ
List of values. Each element is a value of the chosen error function
 .
.Example:
J = ADD.get("CostFunctionJ")[:]
- CostFunctionJAtCurrentOptimum
List of values. Each element is a value of the error function
 .
At each step, the value corresponds to the optimal state found from the
beginning.
.
At each step, the value corresponds to the optimal state found from the
beginning.Example:
JACO = ADD.get("CostFunctionJAtCurrentOptimum")[:]
- CostFunctionJb
List of values. Each element is a value of the error function
 ,
that is of the background difference part. If this part does not exist in the
error function, its value is zero.
,
that is of the background difference part. If this part does not exist in the
error function, its value is zero.Example:
Jb = ADD.get("CostFunctionJb")[:]
- CostFunctionJbAtCurrentOptimum
List of values. Each element is a value of the error function
 . At
each step, the value corresponds to the optimal state found from the
beginning. If this part does not exist in the error function, its value is
zero.
. At
each step, the value corresponds to the optimal state found from the
beginning. If this part does not exist in the error function, its value is
zero.Example:
JbACO = ADD.get("CostFunctionJbAtCurrentOptimum")[:]
- CostFunctionJo
List of values. Each element is a value of the error function
 ,
that is of the observation difference part.
,
that is of the observation difference part.Example:
Jo = ADD.get("CostFunctionJo")[:]
- CostFunctionJoAtCurrentOptimum
List of values. Each element is a value of the error function
 ,
that is of the observation difference part. At each step, the value
corresponds to the optimal state found from the beginning.
,
that is of the observation difference part. At each step, the value
corresponds to the optimal state found from the beginning.Example:
JoACO = ADD.get("CostFunctionJoAtCurrentOptimum")[:]
- CurrentOptimum
List of vectors. Each element is the optimal state obtained at the usual step of the iterative algorithm procedure of the optimization algorithm. It is not necessarily the last state.
Example:
xo = ADD.get("CurrentOptimum")[:]
- CurrentState
List of vectors. Each element is a usual state vector used during the iterative algorithm procedure.
Example:
xs = ADD.get("CurrentState")[:]
- ForecastCovariance
Liste of matrices. Each element is a forecast state error covariance matrix predicted by the model during the time iteration of the algorithm used.
Example :
pf = ADD.get("ForecastCovariance")[-1]
- ForecastState
List of vectors. Each element is a state vector forecasted by the model during the iterative algorithm procedure.
Example:
xf = ADD.get("ForecastState")[:]
- IndexOfOptimum
List of integers. Each element is the iteration index of the optimum obtained at the current step of the iterative algorithm procedure of the optimization algorithm. It is not necessarily the number of the last iteration.
Example:
ioo = ADD.get("IndexOfOptimum")[-1]
- InnovationAtCurrentAnalysis
List of vectors. Each element is an innovation vector at current analysis. This quantity is identical to the innovation vector at analysed state in the case of a single-state assimilation.
Example:
da = ADD.get("InnovationAtCurrentAnalysis")[-1]
- InnovationAtCurrentState
List of vectors. Each element is an innovation vector at current state before analysis.
Example:
ds = ADD.get("InnovationAtCurrentState")[-1]
- SimulatedObservationAtCurrentAnalysis
List of vectors. Each element is an observed vector simulated by the observation operator from the current analysis, that is, in the observation space. This quantity is identical to the observed vector simulated at current state in the case of a single-state assimilation.
Example:
hxs = ADD.get("SimulatedObservationAtCurrentAnalysis")[-1]
- SimulatedObservationAtCurrentOptimum
List of vectors. Each element is a vector of observation simulated from the optimal state obtained at the current step the optimization algorithm, that is, in the observation space.
Example:
hxo = ADD.get("SimulatedObservationAtCurrentOptimum")[-1]
- SimulatedObservationAtCurrentState
List of vectors. Each element is an observed vector simulated by the observation operator from the current state, that is, in the observation space.
Example:
hxs = ADD.get("SimulatedObservationAtCurrentState")[-1]