14.11. Checking algorithm “SamplingTest”¶

14.11.1. Description¶

This test algorithm is used to establish the collection of values of an error functional $J$ of type $L^1$ , $L^2$ or $L^{\infty}$ , with or without weights, using the observation operator $\mathcal{H}$ , for an a priori given sample of states $\mathbf{x}$ . The default error functional is the augmented weighted least squares functional, classically used in data assimilation, using in addition to observations $\mathbf{y}^o$ .

This test is useful for analyzing the sensitivity of the functional $J$ to variations in the state $\mathbf{x}$ in particular.

The sampling of the states $\mathbf{x}$ can be given explicitly or under form of hypercubes, explicit or sampled according to classic distributions, or using Latin hypercube sampling (LHS) or Sobol sequences. The computations are optimized according to the computer resources available and the options requested by the user. You can refer to the Requirements for describing a state sampling for an illustration of sampling. Beware of the size of the hypercube (and then to the number of computations) that can be reached, it can grow quickly to be quite large. When a state is not observable, a “NaN” value is returned.

It is also possible to supply a set of simulations $\mathbf{y}$ already established elsewhere (so there’s no explicit need for an operator $\mathcal{H}$ ), which are implicitly associated with a set of state samples $\mathbf{x}$ . In this case where the set of simulations is provided, it is imperative to also provide the set of states $\mathbf{x}$ by explicit sampling, whose state order corresponds to the order of the simulations $\mathbf{y}$ .

To access the calculated information, the results of the sampling or simulations must be requested explicitly to avoid storage difficulties (if no results are requested, nothing is available). One use for that, on the desired variable, the final saving through “UserPostAnalysis” or the treatment during the calculation by well suited “observer”.

14.11.2. Optional and required commands¶

The general required commands, available in the editing user graphical or textual interface, are the following:

CheckingPoint: Vector. The variable indicates the vector used as the state around which to perform the required check, noted $\mathbf{x}$ and similar to the background $\mathbf{x}^b$ . It is defined as a “Vector” or “VectorSerie” type object. Its availability in output is conditioned by the boolean “Stored” associated with input.

BackgroundError: Matrix. This indicates the background error covariance matrix, previously noted as $\mathbf{B}$ . Its value is defined as a “Matrix” type object, a “ScalarSparseMatrix” type object, or a “DiagonalSparseMatrix” type object, as described in detail in the section Requirements to describe covariance matrices. Its availability in output is conditioned by the boolean “Stored” associated with input.

Observation: List of vectors. The variable indicates the observation vector used for data assimilation or optimization, and usually noted $\mathbf{y}^o$ . Its value is defined as an object of type “Vector” if it is a single observation (temporal or not) or “VectorSeries” if it is a succession of observations. Its availability in output is conditioned by the boolean “Stored” associated in input.

ObservationError: Matrix. The variable indicates the observation error covariance matrix, usually noted as 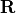$\mathbf{R}$ . It is defined as a “Matrix” type object, a “ScalarSparseMatrix” type object, or a “DiagonalSparseMatrix” type object, as described in detail in the section Requirements to describe covariance matrices. Its availability in output is conditioned by the boolean “Stored” associated with input.

ObservationOperator: Operator. The variable indicates the observation operator, usually noted as $H$ , which transforms the input parameters $\mathbf{x}$ to results $\mathbf{y}$ to be compared to observations $\mathbf{y}^o$ . Its value is defined as a “Function” type object or a “Matrix” type one. In the case of “Function” type, different functional forms can be used, as described in the section Requirements for functions describing an operator. If there is some control $U$ included in the observation, the operator has to be applied to a pair $(X,U)$ .

The general optional commands, available in the editing user graphical or textual interface, are indicated in List of commands and keywords for an ADAO checking case. Moreover, the parameters of the command “AlgorithmParameters” allow to choose the specific options, described hereafter, of the algorithm. See Description of options of an algorithm by “AlgorithmParameters” for the good use of this command.

The options are the following:

EnsembleOfSnapshots

List of vectors or matrix. This key contains an ordered collection of physical state vectors $\mathbf{y}$ (called “snapshots” in reduced basis terminology), with one full state per column if it is a matrix, or one full state per element if it is a list. Caution: the numbering of the support or points, on which or to which a state value is given in each vector, is implicitly that of the natural order of numbering of the state vector, from 0 to the “size minus 1” of this vector.

Example : {"EnsembleOfSnapshots":[y1, y2, y3...]}

QualityCriterion

Predefined name. This key indicates the quality criterion, minimized to find the optimal state estimate. The default is the usual data assimilation criterion named “DA”, the augmented weighted least squares. The possible criterion has to be in the following list, where the equivalent names are indicated by the sign “<=>”: [“AugmentedWeightedLeastSquares” <=> “AWLS” <=> “DA”, “WeightedLeastSquares” <=> “WLS”, “LeastSquares” <=> “LS” <=> “L2”, “AbsoluteValue” <=> “L1”, “MaximumError” <=> “ME” <=> “Linf”]. See the section for Going further in the state estimation by optimization methods to have a detailed definition of these quality criteria.

Example: {"QualityCriterion":"DA"}

SampleAsExplicitHyperCube

List of list of real values. This key describes the calculations points as an hyper-cube, from a given list of explicit sampling of each variable as a list. That is then a list of lists, each of them being potentially of different size. By nature, the points are included in the domain defined by the bounds of the explicit lists for each variable.

Example : {"SampleAsExplicitHyperCube":[[0.,0.25,0.5,0.75,1.], [-2,2,1]]} for a state space of dimension 2.

SampleAsIndependantRandomVariables

List of triplets [Name, Parameters, Number]. This key describes the calculations points as an hyper-cube, for which the points on each axis come from a independent random sampling of the axis variable, under the specification of the distribution, its parameters and the number of points in the sample, as a list ['distribution', [parameters], number] for each axis. The possible distributions are ‘normal’ of parameters (mean,std), ‘lognormal’ of parameters (mean,sigma), ‘uniform’ of parameters (low,high), or ‘weibull’ of parameter (shape). That is then a list of the same size than the one of the state. By nature, the points are included in the unbounded or bounded domain, depending on the characteristics of the distributions chosen for each variable.

Example : {"SampleAsIndependantRandomVariables":[['normal',[0.,1.],3], ['uniform',[-2,2],4]]} for a state space of dimension 2.

SampleAsMinMaxLatinHyperCube

List of triplets of pair values. This key describes the bounded domain in which the calculations points will be placed, from a [min,max] pair for each state component. The lower bounds are included. This list of pairs, identical in number to the size of the state space, is augmented by a pair of integers [dim,nbr] containing the dimension of the state space and the desired number of sample points. Sampling is then automatically constructed using the Latin hypercube method (LHS). By nature, the points are included in the domain defined by the explicit bounds.

Example : {"SampleAsMinMaxLatinHyperCube":[[0.,1.],[-1,3]]+[[2,11]]} for a state space of dimension 2 and 11 sampling points.

SampleAsMinMaxSobolSequence

List of triplets of pair values. This key describes the bounded domain in which the calculations points will be placed, from a [min,max] pair for each state component. The lower bounds are included. This list of pairs, identical in number to the size of the state space, is augmented by a pair of integers [dim,nbr] containing the dimension of the state space and the minimum desired number of sample points (by construction, the number of points generated in the Sobol sequence will be the power of 2 immediately above this minimum number). Sampling is then automatically constructed using the Sobol sequence method. By nature, the points are included in the domain defined by the explicit bounds.

Remark: it is required to have Scipy version 1.7.0 or higher to use this sampling option.

Example : {"SampleAsMinMaxSobolSequence":[[0.,1.],[-1,3]]+[[2,11]]} for a state space of dimension 2 and 11 sampling points (there will be 16 points in practice).

SampleAsMinMaxStepHyperCube

List of triplets of real values. This key describes the calculations points as an hyper-cube, from a given list of implicit sampling of each variable by a triplet [min,max,step]. That is then a list of the same size than the one of the state. The bounds are included. By nature, the points are included in the domain defined by the explicit bounds.

Example : {"SampleAsMinMaxStepHyperCube":[[0.,1.,0.25],[-1,3,1]]} for a state space of dimension 2.

SampleAsnUplet

List of states. This key describes the calculations points as a list of n-uplets, each n-uplet being a state. By nature, points are included in the bounded domain defined as the convex envelope of explicitly designated points.

Example : {"SampleAsnUplet":[[0,1,2,3],[4,3,2,1],[-2,3,-4,5]]} for 3 points in a state space of dimension 4.

SetDebug

Boolean value. This variable leads to the activation, or not, of the debug mode during the function or operator evaluation. The default is “False”, the choices are “True” or “False”.

Example: {"SetDebug":False}

SetSeed

Integer value. This key allow to give an integer in order to fix the seed of the random generator used in the algorithm. By default, the seed is left uninitialized, and so use the default initialization from the computer, which then change at each study. To ensure the reproducibility of results involving random samples, it is strongly advised to initialize the seed. A simple convenient value is for example 123456789. It is recommended to put an integer with more than 6 or 7 digits to properly initialize the random generator.

Example: {"SetSeed":123456789}

StoreSupplementaryCalculations

List of names. This list indicates the names of the supplementary variables, that can be available during or at the end of the algorithm, if they are initially required by the user. Their availability involves, potentially, costly calculations or memory consumptions. The default is then a void list, none of these variables being calculated and stored by default (excepted the unconditional variables). The possible names are in the following list (the detailed description of each named variable is given in the following part of this specific algorithmic documentation, in the sub-section “Information and variables available at the end of the algorithm”): [ “CostFunctionJ”, “CostFunctionJb”, “CostFunctionJo”, “CurrentState”, “EnsembleOfSimulations”, “EnsembleOfStates”, “Innovation”, “InnovationAtCurrentState”, “SimulatedObservationAtCurrentState”, ].

Example : {"StoreSupplementaryCalculations":["CurrentState", "Residu"]}

14.11.3. Information and variables available at the end of the algorithm¶

At the output, after executing the algorithm, there are information and variables originating from the calculation. The description of Variables and information available at the output show the way to obtain them by the method named get, of the variable “ADD” of the post-processing in graphical interface, or of the case in textual interface. The input variables, available to the user at the output in order to facilitate the writing of post-processing procedures, are described in the Inventory of potentially available information at the output.

Permanent outputs (non conditional)

The unconditional outputs of the algorithm are the following:

CostFunctionJ

List of values. Each element is a value of the chosen error function $J$ .

Example: J = ADD.get("CostFunctionJ")[:]

CostFunctionJb

List of values. Each element is a value of the error function $J^b$ , that is of the background difference part. If this part does not exist in the error function, its value is zero.

Example: Jb = ADD.get("CostFunctionJb")[:]

CostFunctionJo

List of values. Each element is a value of the error function $J^o$ , that is of the observation difference part.

Example: Jo = ADD.get("CostFunctionJo")[:]

Set of on-demand outputs (conditional or not)

The whole set of algorithm outputs (conditional or not), sorted by alphabetical order, is the following:

CostFunctionJ

List of values. Each element is a value of the chosen error function $J$ .

Example: J = ADD.get("CostFunctionJ")[:]

CostFunctionJb

List of values. Each element is a value of the error function $J^b$ , that is of the background difference part. If this part does not exist in the error function, its value is zero.

Example: Jb = ADD.get("CostFunctionJb")[:]

CostFunctionJo

List of values. Each element is a value of the error function $J^o$ , that is of the observation difference part.

Example: Jo = ADD.get("CostFunctionJo")[:]

CurrentState

List of vectors. Each element is a usual state vector used during the iterative algorithm procedure.

Example: xs = ADD.get("CurrentState")[:]

EnsembleOfSimulations

List of vectors or matrix. This key contains an ordered collection of physical or simulated state vectors $\mathbf{y}$ (called “snapshots” in reduced basis terminology), with 1 state per column if it is a matrix, or 1 state per element if it is a list. Caution: the numbering of the support or points, on which or to which a state value is given in each vector, is implicitly that of the natural order of numbering of the state vector, from 0 to the “size minus 1” of this vector.

Example : {"EnsembleOfSimulations":[y1, y2, y3...]}

EnsembleOfStates

List of vectors or matrix. Each element is an ordered collection of physical or parameter state vectors $\mathbf{x}$ , with 1 state per column if it is a matrix, or 1 state per element if it is a list. Caution: the numbering of the support or points, on which or to which a state value is given in each vector, is implicitly that of the natural order of numbering of the state vector, from 0 to the “size minus 1” of this vector.

Example : {"EnsembleOfStates":[x1, x2, x3...]}

Innovation

List of vectors. Each element is an innovation vector, which is in static the difference between the optimal and the background, and in dynamic the evolution increment.

Example: d = ADD.get("Innovation")[-1]

InnovationAtCurrentState

List of vectors. Each element is an innovation vector at current state before analysis.

Example: ds = ADD.get("InnovationAtCurrentState")[-1]

SimulatedObservationAtCurrentState

List of vectors. Each element is an observed vector simulated by the observation operator from the current state, that is, in the observation space.

Example: hxs = ADD.get("SimulatedObservationAtCurrentState")[-1]

14.11.4. See also¶

References to other sections:

References to other SALOME modules:

OPENTURNS, see the User guide of OPENTURNS module in the main “Help” menu of SALOME platform